Triacontahexaèdre tétragonal

TRIACONTAHEXAÈDRE TÉTRAGONAL
Tetragonal triacontahexahedron, Tetragontriakontahexaheder


Image d'Alain Esculier	Image de Guy Valette

Famille

polyèdre ayant les symétries du cube (mais non semi-régulier)

Historique

???

Etymologie

triacontahexa = 36 ; les faces sont des tétragones.

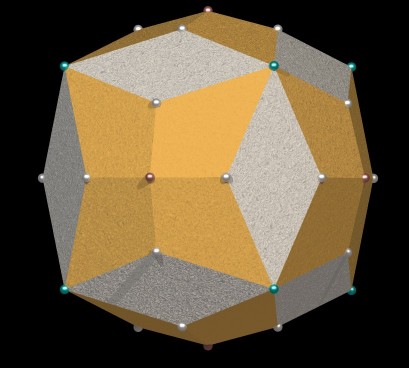
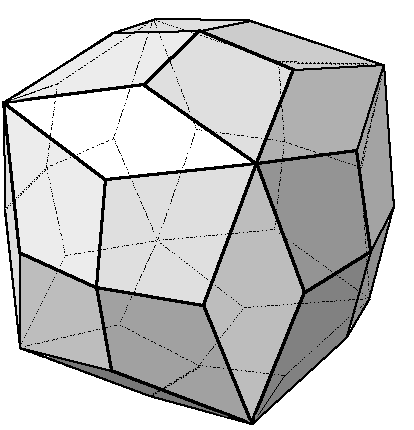
Faces

36 faces : 12 losanges et 24 cerfs-volants.

Sommets

38 sommets, dont 24 sommets de degré 3, de code de Schläfli 4³ , 8 sommets de degré 4 de code 4⁴ et 6 sommets de degré 6 de code 4⁶.

Arêtes

72 arêtes

Construction

Octaèdre tronquééaugmenté sur chaque face d'une pyramide droite (8 pyramides carrées et 6 hexagonales)
Tétraki hexaèdre augmenté sur chaque face d'une pyramide droite (24 pyramides triangulaires)
Somme d'un octaèdre tronqué (en rouge ci-contre) et de son dual le tétraki hexaèdre (en jaune ci-contre)

Coordonnées
des sommets

24 sommets de l'octaèdre tronqué : (+-a, +-2a, 0) et permutés
8 sommets des pyramides hexagonales : (+-b,+-b,+-b) et permutés (formant un cube)
6 sommets des pyramides carrées : (+-c,0,0) et permutés (formant un octaèdre)
avec 2b = 3a et 4c = 9a

Groupe des isométries

= celui du cube ; 3 orbites de sommets, 2 orbites d'arêtes et 2 orbites de faces.

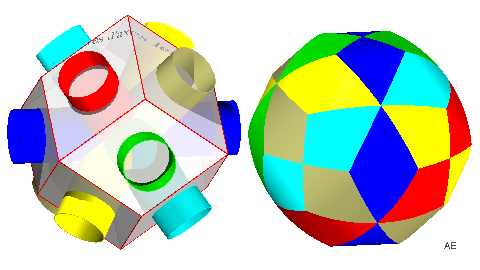
L'intersection de 6 cylindres de révolution pleins identiques dont les axes sont les diagonales d'un cuboctaèdre (ou les diagonales faciales d'un dodécaèdre rhombique) forme un solide de Steinmetz dont la surface a une structure de triacontahexaèdre tétragonal (chaque cylindre forme un ruban composé de 6 "faces" du (faux) polyèdre) :