SOLIDE DE STEINMETZ
Steinmetz solid, Steinmetzfestkörper
.png)
| polyèdre suivant | polyèdre précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
SOLIDE DE STEINMETZ
Steinmetz solid, Steinmetzfestkörper
.png)
| Notion étudiée par Steinmetz en ... .
Charles Steinmetz (1865-1923) : mathématicien américain. Voir plus de détails sur : baumanneduard.ch, mathworld.wolfram.com, en.wikipedia.org. |
| Les solides de Steinmetz sont les intersections de cylindres de révolution pleins d'axes concourants et de même diamètre. |

Cas de deux cylindres orthogonaux |
Pour n cylindres, on obtient un solide dont la
surface est réunion de portions de cylindres formant n anneaux
correspondant à chacun des cylindres (dessinés de couleurs
différentes ci-dessous).
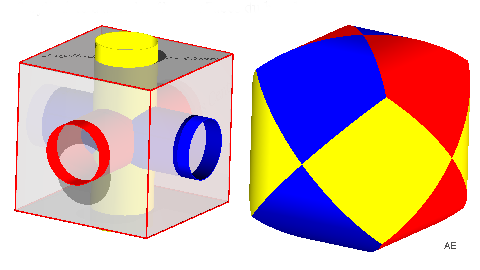 Faces : 12 (3 anneaux à 4 faces) La surface obtenue est topologiquement équivalente à celle du dodécaèdre rhombique |
Axes : 4 diagonales faciales de l'octaèdre (ou
sommitales du cube)
|
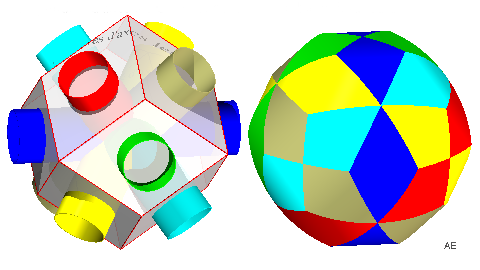 Faces : 36 (6 anneaux à 6 faces) Équivalence : triacontahexaèdre tétragonal |
 Faces : 60 (6 anneaux à 10 faces) Équivalence : hexacontaèdre trapézoïdal |
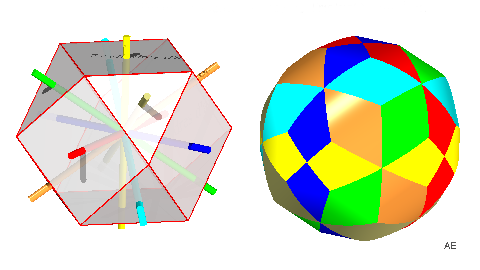 Faces : 48 (3 anneaux à 8 faces et 4 anneaux à 6 faces) Équivalence : |
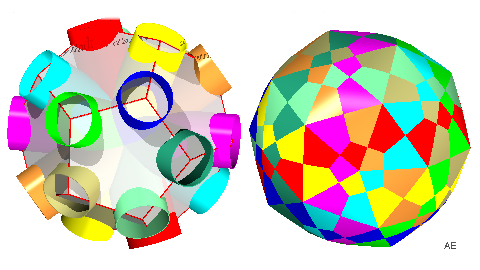 Faces : (10 anneaux à ... faces) Équivalence : |
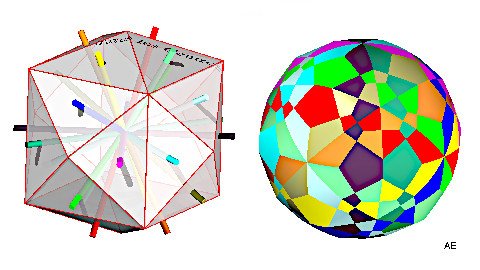 Faces : 240 (12 anneaux à 20 faces) |
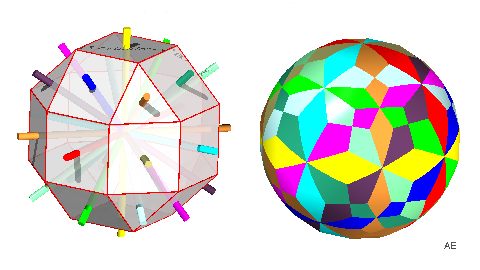 Faces : |
| Lorsque les cylindres ont des axes situés dans un même plan disposés de façon régulière, la surface du solide de Steinmetz est, à dilatation près, un équidomoïde. |
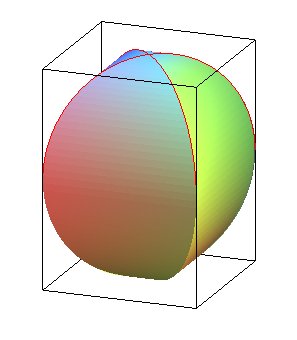 |
| Le rulpidon
d'Ulysse Lacoste est un solide de Steinmetz percé de deux cylindres
pleins.
il possède 10 arêtes qui sont 5 bicylindriques. Équation : |
 |
| polyèdre suivant | polyèdre précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2023