ÉQUIDOMOÏDE
Equidomoid
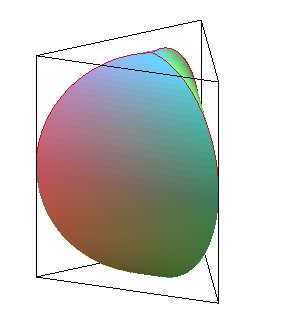
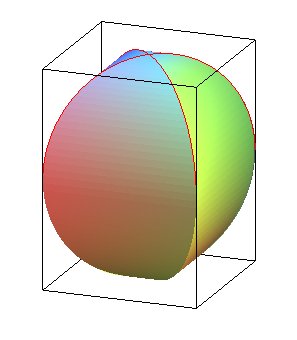
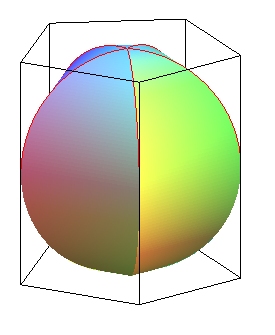
Équidomoïdes d'ordres 3, 4 et 5
| polyèdre suivant | polyèdre précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
ÉQUIDOMOÏDE
Equidomoid



Équidomoïdes d'ordres 3, 4 et 5
| Forme étudiée par Archimède, puis
entre 1867 et 1875 par Léopold
Hugo, neveu de Victor, qui lui a donné ce nom.
Autre nom : dôme d'Archimède. Ref : Émile Fourrey, récréations géométriques, p 319 à 326. |
Un équidomoïde d'ordre n est
une figure obtenue en remplaçant dans un prisme
droit à bases régulières d'ordre n, de hauteur
2R égale au diamètre des bases, les faces latérales
par une portion de cylindre
elliptique droit (appelée onglet) dont l'axe passe par le centre
du prisme s'appuyant sur des armatures circulaires. L'équidomoïde
n'est donc pas un polyèdre au sens strict.
L'ellipse des cylindres, de demi-axes R et ,
tend vers un cercle lorsque n tend vers l'infini ; l'équidomoïde
tend alors vers une sphère de rayon R (alors que le prisme
circonscrit tend vers une portion de cylindre de révolution).
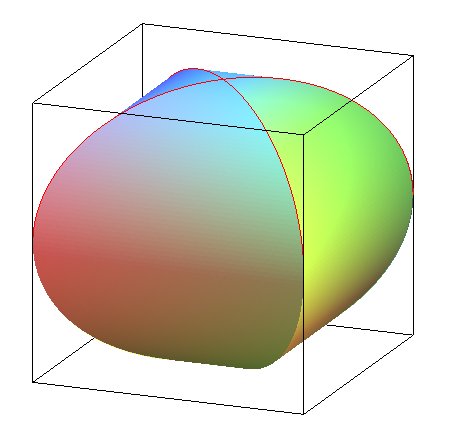
| Pour n pair, si l'on effectue une dilatation verticale
de rapport |
 |
| On peut étendre la notion d'équidomoïde au cas de prismes croisés : |
 |

Le dôme de la cathédrale de Florence est
un demi-pseudo-équidomoïde octogonal, avec des armatures elliptiques
plutôt que circulaires.
|

Les caramboles ont une forme d'équidomoïde pentagonal étoilé. |
Voir aussi l'oloïde.

Divers équidomoïdes, par Alain Esculier
| polyèdre suivant | polyèdre précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL
2024