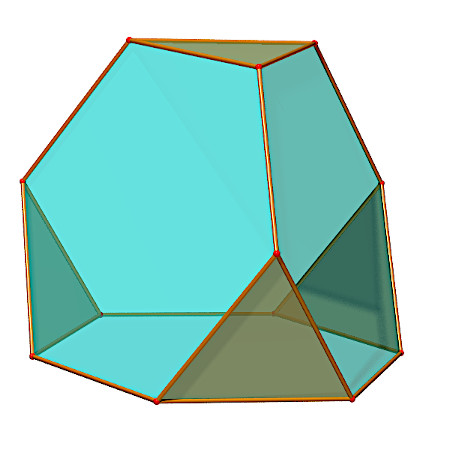
Tétraèdre tronqué

TÉTRAÈDRE TRONQUÉ
Truncated tetrahedron, abgestumpftesTetraeder

Vues Povray de cette page réalisées par Alain Esculier.

Famille

polyèdre semi-régulier, ou polyèdre d'Archimède

Historique

solide connu d'Archimède (III^e s. av. J.C.)

Dual

triaki-tétraèdre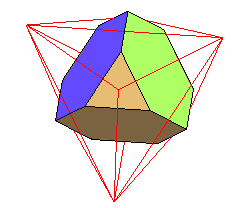

Faces

4 triangles et 4 hexagones ; c'est donc un octaèdre.

Sommets

12 sommets de degré 3, de code de Schläfli 3.6² .

Arêtes

18 arêtes de longueur a ;
angle dièdre entre 2 hexagones : arccos 1/3 = 70° 31' 44" ;
angle dièdre entre 1 hexagone et 1 triangle : arccos(–1/3) = 109° 28' 16"

Patron

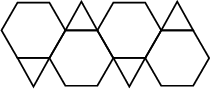(261 patrons en tout)

Graphe

Diamètres

sphère inscrite dans les hexagones :

, dans les triangles :

;
intersphère (tangente aux arêtes):

; sphère circonscrite :

Mensurations

volume :

aire :

coefficient isopérimétrique :

Coordonnées
des sommets

et les permutés, avec un nombre pair de signes -.

Construction

tétraèdre faiblement tronqué

polyèdre dérivé

tétraèdre tronqué augmenté
tétraèdre étoilé de Jamnitzer, voir au bas de cette page

Plans de symétrie

Axes de rotation

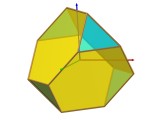3 axes passant par les milieux de 2 arêtes opposées joignant des hexagones (1 rotation d'ordre 2 par axe)
4 axes passant par les centres de 2 faces opposées (2 rotations d'ordre 3 par axe)

Groupe des isométries

= celui du tétraèdre .

On peut paver l'espace avec un réseau de tétraèdres tronqués placés hexagones contre hexagones, et en "bouchant les trous" par des tétraèdres régulier.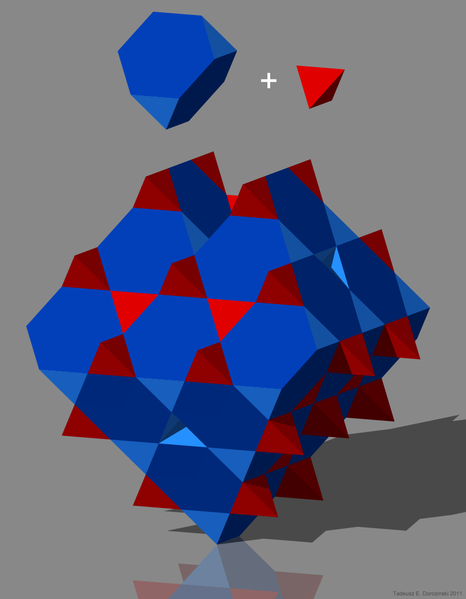

Image tirée de Wikipedia.

Cette horloge solaire du XVIème siècle, visible au musée Galilée à Florence a une forme de tétraèdre tronqué.