| polyèdre suivant | polyèdre précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
POLYÈDRE, PAVAGE, TRONQUÉ AUX SOMMETS
vertice truncated polyhedron or tiling, eckenabgestumpftes
Polyeder oder Parkettierung
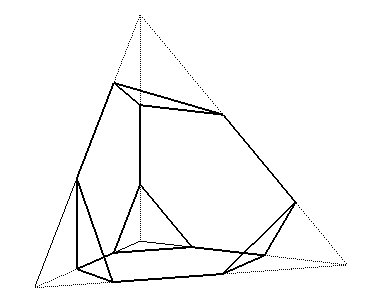
| Un polyèdre est dit être obtenu par troncature des sommets d'un polyèdre convexe s'il résulte de la suppression dans ce dernier de pyramides en chaque sommet, les diverses pyramides ne devant se toucher éventuellement qu'en leurs sommets. |  |
| On parle de troncature forte (ou de rectification)
lorsque les arêtes des pyramides sont les moitiés des arêtes
du polyèdre de départ.
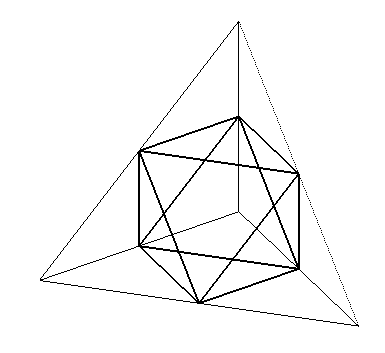
Pour qu'un polyèdre (P0) admette une troncature forte, il faut et il suffit que, pour tout sommet A de P0, les sommets voisins de A soient coplanaires. Cette condition est en particulier réalisée dans les deux cas suivants : tous les sommets de P0 sont de degré 3; P0 est un polyèdre IFR. Chaque face du polyèdre de départ (P0) est alors remplacée par une face ayant le même ordre, et il apparait S nouvelles faces, dont l'ordre est le degré du sommet tronqué. Si S0, F0, A0 sont les nombres de sommets, de faces et
d'arêtes de (P0), on a :
Les troncatures fortes d'un polyèdre et de son dual, si elles existent, sont équivalentes. |
 |
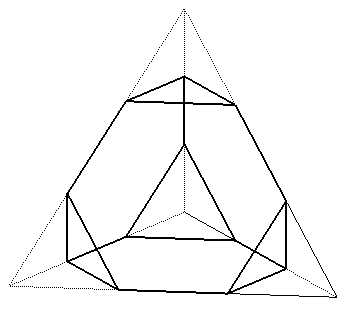
| On parle de troncature faible lorsque les arêtes
des pyramides ont une longueur égale à k fois celles
des arêtes du polyèdre de départ, avec k <
1/2 (même remarque que ci-dessus quant à l'existence du polyèdre
tronqué).
Pour qu'une face régulière d'ordre n donne par troncature un face régulière, il faut prendre Chaque face du polyèdre de départ (P0) est alors remplacée par une face dont l'ordre a doublé, et il apparait S nouvelles faces, dont l'ordre est le degré du sommet tronqué. Si S0, F0, A0 sont les nombres de sommets, de faces et
d'arêtes de (P0), on a :
|
 |
Exemples : les 5 polyèdres réguliers fournissent,
par troncature forte ou faible, 7 des 13 polyèdres archimédiens
:
| Polyèdre de départ | Polyèdre fortement tronqué aux sommets (ou rectifié) | Polyèdre faiblement tronqué aux sommets |
| polyèdre régulier de code pq (à chaque sommet arrivent q p-gones) | polyèdre semi-régulier de code q. (p)2 | polyèdre semi-régulier de code q. (2p)2 |
| tétraèdre régulier |
octaèdre régulier |
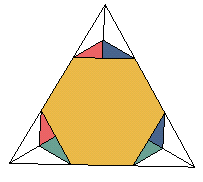
tétraèdre tronqué (k = 1/3) |
| cube |
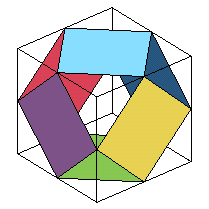
cuboctaèdre |
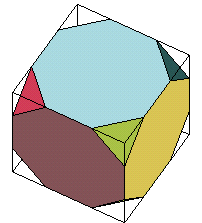
cube tronqué ( |
| octaèdre régulier |
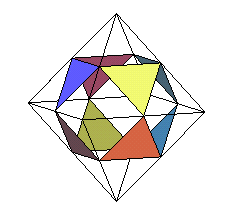
cuboctaèdre |
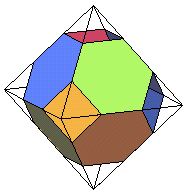
octaèdre tronqué (k = 1/3) |
| dodécaèdre régulier |
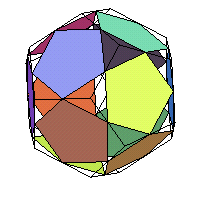
icosidodécaèdre |
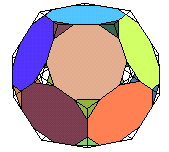
dodécaèdre tronqué . |
| icosaèdre régulier |
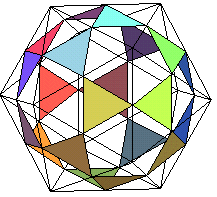
icosidodécaèdre |
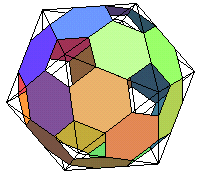
icosaèdre tronqué (k = 1/3) |
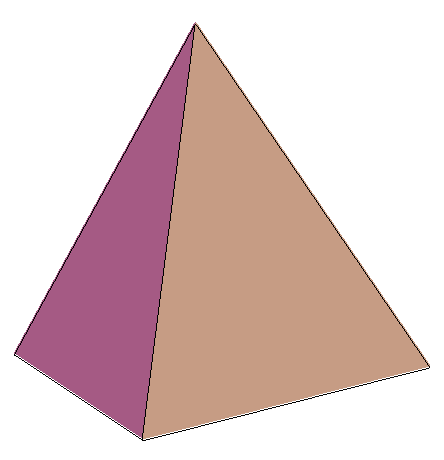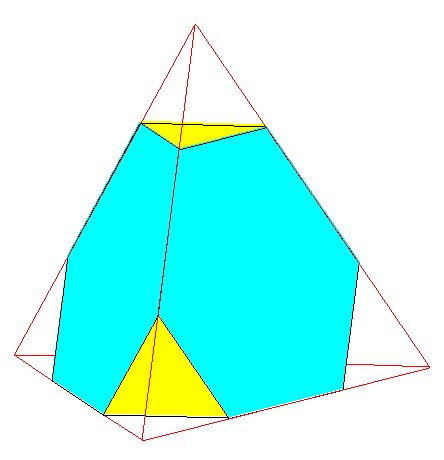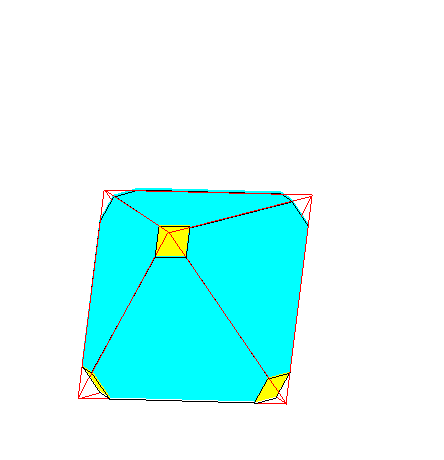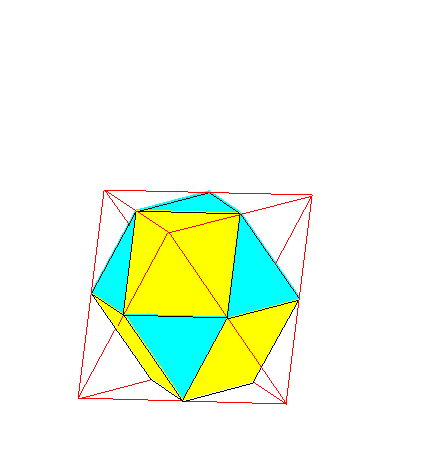 |
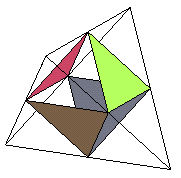
En partant d'un tétrèdre régulier,
observer les troncatures successives :
-tétraèdre tronqué,
|
Exemples des troncatures faibles et fortes des 3 pavages
réguliers, fournissant 4 des 8 pavages
semi-réguliers :
|
|
|
|
|

Pavage triangulaire (en bleu : dual du pavage hexagonal rouge) |

Pavage hexagonal |

Pavage trihexagonal |

Premier arrêt lorsque tous les pavés (hexagones centraux et pentagones à bordures rouges et bleues) ont même aire. |

Pavage carré (en bleu : dual du pavage carré en rouge) |

Pavage carré tronqué |

De nouveau le pavage carré |

Deuxième arrêt lorsque tous les pavés (carrés centraux et pentagones à bordures rouges et bleues) ont même aire. |
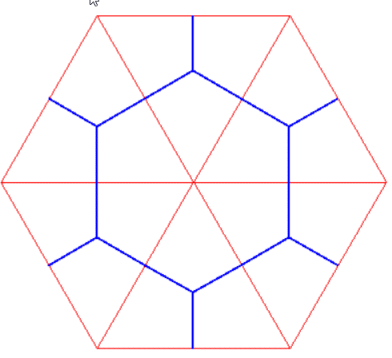
Pavage hexagonal (en bleu : dual du pavage triangulaire en rouge) |

Pavage hexagonal tronqué |

Pavage trihexagonal |
 |
Les polyèdres obtenus par troncature des polyèdres
semi-réguliers ne sont plus semi-réguliers, mais certains
sont équivalents à des polyèdres semi-réguliers
:
| Départ | troncature forte | troncature faible |
| cuboctaèdre |
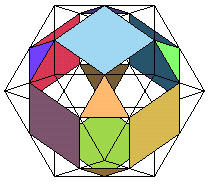 |
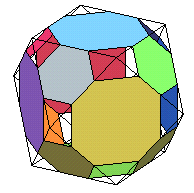 k = 1/3 : seules les faces hexagonales sont régulières |
| icosidodécaèdre |
 |
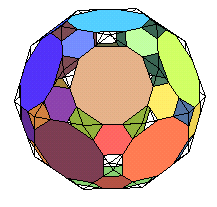 k = 1/3 : seules les faces hexagonales sont régulières |
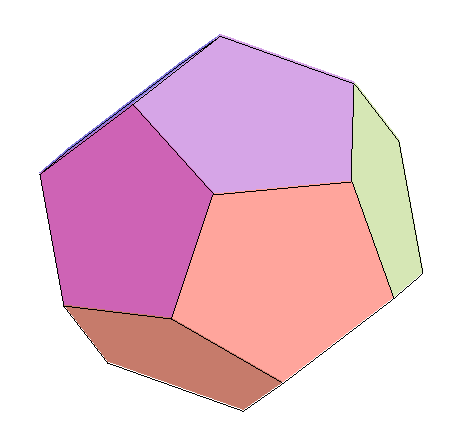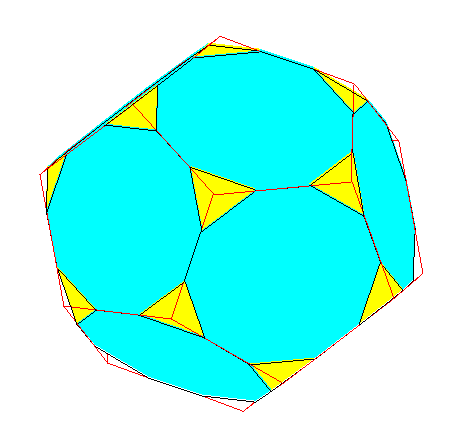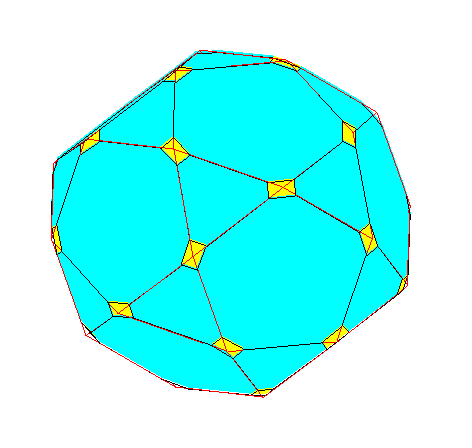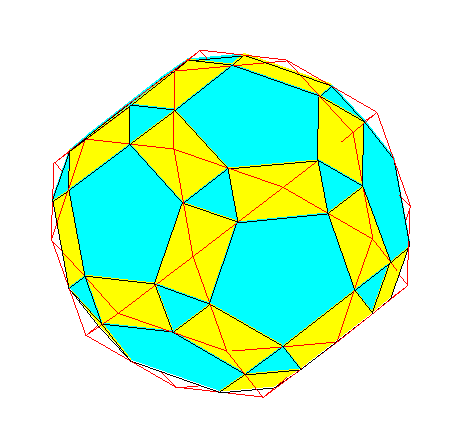 |
Observer successivement
dodécaèdre, dodécaèdre tronqué, icosidodécaèdre, pseudo-icosidodécaèdre tronqué pseudo-rhombicosidodécaèdre |
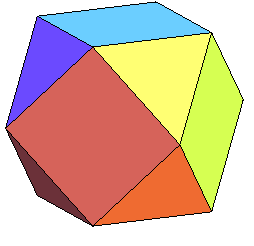
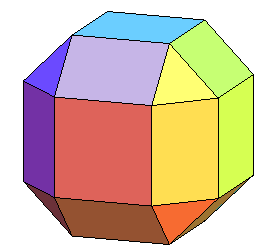
Voici les résultats des troncatures fortes successives
du cube :
à partir de l'étape 5, les faces obtenues ne sont plus
planes, et le solide obtenu n'est plus à proprement parler un polyèdre.
 |
 |
 |
 |
 |
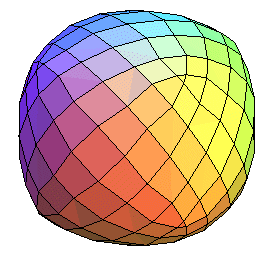 |
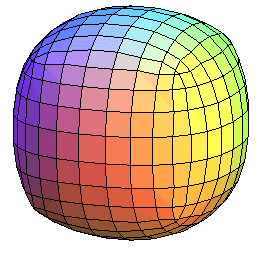 |
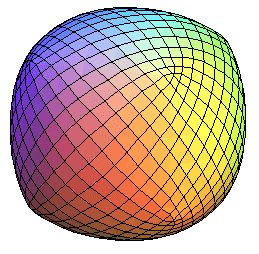 |
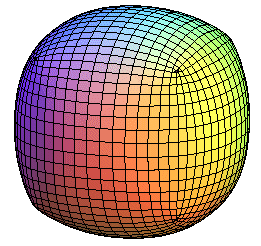
Quelle est la surface limite ???? |
On peut aussi appliquer la troncature aux polyèdres
étoilés à faces non étoilées ; par exemple,
la troncature faible ou forte des 2 polyèdres étoilés
réguliers de Poinsot fournit 4 polyèdres étoilés
semi- réguliers :
| Polyèdre de départ | Polyèdre fortement tronqué | Polyèdre faiblement tronqué |
| grand dodécaèdre |
|
|
| grand icosaèdre |
|
|
Autre méthode de construction de polyèdres
: la troncature des arêtes,
l'augmentation.
Un rhomboèdre à deux sommets opposés tronqués apparait dans la célèbre gravure d'Albert Dürer "melancolia" :
| polyèdre suivant | polyèdre précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2014