| |
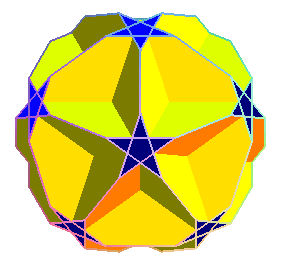
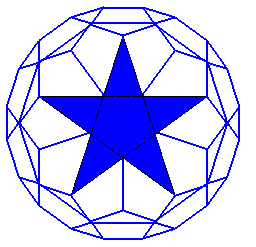
grand dodécaèdre tronqué |
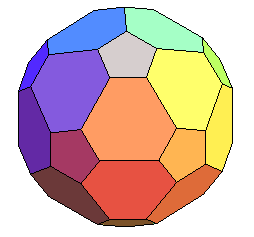
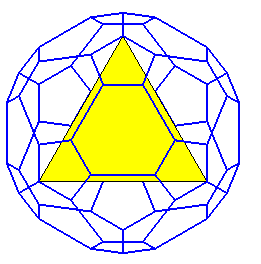
grand rhombicosidodécaèdre |
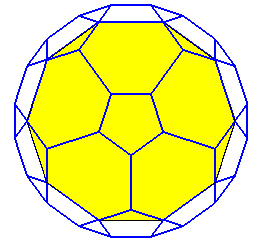
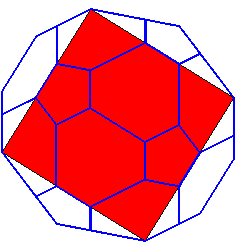
grand dodécicosidodécaèdre |
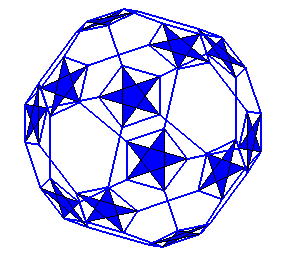
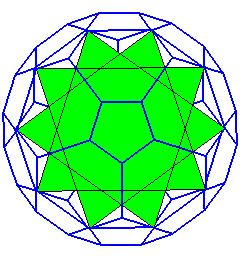
grand rhombidodécaèdre |
| Famille |
polyèdre étoilé
semi-régulier (ou uniforme U37), ou polyèdre
de Badoureau-Coxeter (découvert en fait par J.Pitsch en
1881) |
idem, U67 |
idem, U61 |
idem, U73 |
| Étymologie |
lire : (grand dodécaèdre) tronqué,
et non : grand (dodécaèdre tronqué)
(cf le grand
icosidodécaèdre tronqué pour qui c'est l'inverse
!) |
rhomb car il a des faces carrées, icosi car il
a 20 faces triangulaires, dodéca car il a 12 faces pentagonales,
et grand pour le différencier du rhombicosidodécaèdre
convexe |
dodéc car il a 12 faces pentagonales, icosi car
il a 20 faces triangulaires, dodéca car il a 12 faces décagonales,
et grand pour le différencier du petit |
rhombi car il a des faces carrées, dodéca
car il a 12 faces décagonales, et grand pour le différencier
des polyèdres convexes |
| Dual |
|
|
|
|
| Faces |
12 pentagones étoilés et 12 décagones |
20 triangles, 30 carrés et 12 pentagones étoilés |
20 triangles, 12 pentagones étoilés et
12 décagones étoilés |
30 carrés et 12 décagones étoilés |
| Sommets |
60 sommets , de code
de Schläfli 10.10.5/2 |
60 sommets , de code
de Schläfli 3.4.5/2.4 |
60 sommets, de code
de Schläfli 3.10/3.5/2.10/3 |
60 sommets, de code
de Schläfli 4.10/3.4.10/3 |
| Arêtes |
90 arêtes |
120 arêtes |
idem |
idem |
| Construction |
grand dodécaèdre:faiblement
tronqué. |
mêmes sommets que celui de gauche |
comme U67, les carrés étant remplacés
par les décagones |
comme U67, les triangles et pentagones étant remplacés
par les décagones |
| Groupe des isométries |
celui du dodécaèdre |
idem |
idem |
idem |