+ rang dans la liste des polyèdres uniformes
Symbole de Whytoff
Poincaré
U3
(3/2 3|3)
4 hexagones
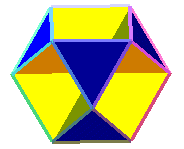
tétrahémihexaèdre
U4
Mêmes sommets et arêtes que l'octaèdre
4.3.4.3
(3/2 3|2)
4 triangles
3 carrés
unilatère

| polyèdre suivant | polyèdre précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
POLYÈDRES DE BADOUREAU-COXETER
Badoureau-Coxeter polyhedra, Badoureau-Coxeter Polyeder
| Albert Badoureau (1853-1923) : ingénieur et mathématicien
français.
Harold Scott MacDonald Coxeter (1907 - 2003) : mathématicien anglais. Polyèdres de Badoureau découverts par ... Badoureau en 1881. Polyèdres de Coxeter découverts par... Coxeter et Miller en 1932 (numéros 32, 40, 43, 46, 50, 57, 60, 64, 69, 72, 74, 75 ci-après). Preuve que ce sont les seuls polyèdres semi-réguliers étoilés par S.P. Sopov en 1970. |
Sites : fr.wikipedia.org/wiki/Liste_des_poly%C3%A8dres_uniformes www.mathconsult.ch/showroom/unipoly/ mathworld.wolfram.com/UniformPolyhedron.html www.singsurf.org/polyhedra/uniform.php www.math.technion.ac.il/~rl/docs/uniform.pdf gratrix.net/polyhedra/uniform/summary/ www.software3d.com/Uniform.php |
Les polyèdres de Badoureau-Coxeter sont les
polyèdres
étoilés non convexes et semi-réguliers
(ou uniformes) non réguliers, autres que les prismes
et les antiprismes.
Ce sont donc les analogues étoilés des
polyèdres archimédiens.
Ils sont au nombre de 53, dont 37 découverts par
Badoureau.
2 ont les symétries du tétraèdre
:
| Nom officiel
+ rang dans la liste des polyèdres uniformes |
construction | code de Schläfli
Symbole de Whytoff |
faces | sommets | Car.
d'Euler
Poincaré |
figure |
| octahémioctaèdre
U3 |
Mêmes sommets et arêtes que le cuboctaèdre | 6.3.6.3
(3/2 3|3) |
8 triangles
4 hexagones |
12 | 0 |
 |
|
tétrahémihexaèdre U4 |
Mêmes sommets et arêtes que l'octaèdre |
4.3.4.3 (3/2 3|2) |
4 triangles 3 carrés |
6 | 1
unilatère |
 |
9 ont les symétries du cube :
| Nom officiel
+ rang dans la liste des polyèdres uniformes |
construction | code de Schläfli
Symbole de Whytoff |
faces | sommets | Caract.
d'Euler Poincaré |
figure |
| petit cubicuboctaèdre U13 | Mêmes sommets et arêtes que le rhombicuboctaèdre | 3.8.4.8
(3 4|4) |
8 triangles
6 carrés 6 octogones |
24 | -4 |
 |
| grand
cubicuboctaèdre
U14 |
Mêmes sommets que le cube tronqué | 3.8/3.4.8/3
(3 4|4/3) |
8 triangles
6 carrés 6 octogones étoilés .................. |
24 | -4 |
 |
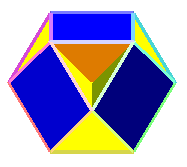
| cubohémioctaèdre
U15 |
Mêmes sommets et arêtes que le cuboctaèdre | 4.6.4.6
(4 4|3) |
6 carrés
4 hexagones |
12 | -2
unilatère |
 |
| cuboctaèdre
cubitronqué
U16 |
Mêmes sommets qu'un "pseudo" cuboctaèdre tronqué | 8/3.6.8
(4/3 3 4|) |
8 hexagones
6 octogones 6 octogones étoilés |
48 | - 4 |
 |
| grand rhombicuboctaèdre U17 | Mêmes sommets que le cube tronqué | 3.43
(3 4|2) |
8 triangles
18 carrés |
24 | 2 |
 |
| petit
rhombihexaèdre
U18 |
Mêmes sommets et arêtes que le rhombicuboctaèdre | 4.8.4.8
(3/2 2 4|) ?? ou (4 4|4) |
12 carrés
6 octogones |
24 | - 6
unilatère |
 |
| cube
tronqué étoilé
U19 |
Mêmes sommets que le rhombicuboctaèdre | 3.(8/3)2
(2 3|4/3) |
8 triangles
6 octogones étoilés |
24 | 2 |
 |
| grand
cuboctaèdre tronqué
U20 |
Mêmes sommets qu'un "pseudo" cuboctaèdre tronqué | 4.6.8/3
(2 3 4/3|) |
12 carrés
8 hexagones 6 octogones étoilés |
48 | 2 |
 |
| grand
rhombihexaèdre
U21 |
Mêmes sommets que le cube tronqué | 8/3.4.8/3.4
2 4/3 (3/2 4/2)
|
12 carrés
6 octogones étoilés |
24 | -6 |
 |
42 ont les symétries du dodécaèdre
:
| Nom officiel
+ rang dans la liste des polyèdres uniformes |
construction | code de Schläfli | faces | sommets | Car.
d'Euler
Poincaré |
figure |
| petit
icosidodécaèdre ditrigonal
U30 |
mêmes sommets que le dodécaèdre | 5/2.3.5/2.3.5/2.3
(3|5/2 3) |
32 | 20 | -8 |  |
| petit
icosicosidodécaèdre
U31 découvert par Pitsch |
mêmes sommets qu'un pseudo rhombicosidodécaèdre | 5/2.6.3.6
(5/2 3|3) |
52 | 60 | -8 |  |
| petit
icosicosidodécaèdre adouci
U32 découvert par Coxeter |
mêmes sommets qu'un pseudo icosaèdre tronqué | 3.5/2.34
(|5/2 3 3) |
112 | 60 | -8 |  |
| petit
dodécicosidodécaèdre
U33 |
mêmes sommets et arêtes que le rhombicosidodécaèdre | 3.10.5.10
(3/2 5|5) |
44 | 60 | -16 |  |
| (grand) dodécadodécaèdre
U36 |
mêmes sommets que l'icosidodécaèdre | (5/2.5)2
(2|5/2 5) |
24 | 30 | -6 |  |
| grand
dodécaèdre tronqué
U37 découvert par Pitsch |
grand dodécaèdre faiblement tronqué | 10.5/2.10
(2 5/2|5) |
24 | 60 | -16 | 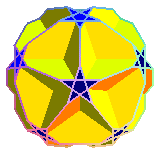 |
| rhombidodécadodécaèdre
U38 |
grand dodécaèdre chanfreiné | 5/2.4.5.4
(5/2 5|2) |
54 | 60 | -6 |  |
| petit
rhombidodécaèdre
U39 |
mêmes sommets et arêtes que le rhombicosidodécaèdre | 4.10.4.10
2 5 (3/2 5/2) |
|
42 | 60 | -18 |  |
| dodécadodécaèdre
adouci
U40 découvert par Coxeter |
3.5/2.3.5.3
(|2 5/2 5) |
84 | 60 | -6 |  |
|
| dodécadodécaèdre
ditrigonal
U41 |
mêmes sommets que le dodécaèdre | 5/2.5.5/2.5.5/2.5
(3|5/2 5) |
24 | 20 | -16 |  |
| grand
dodécicosidodécaèdre ditrigonal
U42 |
mêmes sommets que le dodécaèdre tronqué | 3.10/3.5.10/3
(3 5|5/3) |
44 | 60 | -16 |  |
| petit
dodécicosidodécaèdre ditrigonal
U43 découvert par Coxeter |
mêmes sommets qu'un pseudo rhombicosidodécaèdre | 5/2.10.3.10
(5/2 3|5) |
44 | 60 | -16 | 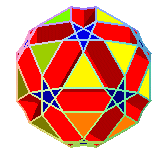 |
| icosidodécadodécaèdre
U44 |
mêmes sommets et arêtes que U38 | 5/2.6.5.6
(5/2 5|3) |
44 | 60 | -16 |  |
| dodécadodécaèdre
icositronqué
U45 |
mêmes sommets qu'un pseudo icosidodécaèdre tronqué | 10/3.6.10
(5/3 3 5|) |
44 | 120 | -16 |  |
| icosidodécadodécaèdre
adouci
U46 découvert par Coxeter |
5/2.33.5.3
(|5/3 3 5) |
104 | 60 | -16 |  |
|
| grand
icosidodécaèdre ditrigonal
U47 |
mêmes sommets que le dodécaèdre | (3.5)3
(3/2|3 5) ? |
32 | 20 | -8 |  |
| grand
icosicosidodécaèdre
U48 |
mêmes sommets que le dodécaèdre tronqué | 3.6.5.6
(3/2 5|3) |
52 | 60 | -8 | 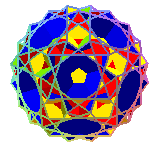 |
| petit icosihémidodécaèdre U49 | mêmes sommets et arêtes que l'icosidodécaèdre | 3.10.3.10
(3/2 3|5) |
26 | 30 | -4 |  |
| petit
dodécicosaèdre
U50 découvert par Coxeter |
mêmes sommets qu'un pseudo rhombicosidodécaèdre | 6.10.6.10
3 5 (3/2 5/4) |
|
32 | 60 | -28 |  |
| petit
dodécahémidodécaèdre
U51 |
mêmes sommets et arêtes que l'icosidodécaèdre | 5.10.5.10
(5 5|5) |
18 | 30 | -12 |  |
| grand
icosidodécaèdre
U54 |
grand icosaèdre fortement tronqué | (5/2.3)2
(2|5/2 3) |
32 | 30 | 2 |  |
| grand
icosaèdre tronqué
U55 découvert par Pitsch |
grand icosaèdre tronqué | 6.5/2.6
(2 5/2|3) |
32 | 60 | 2 |  |
| rhombicosaèdre
U56 |
mêmes sommets et arêtes que U38 | 4.6.4.6
2 3 (5/4 5/2) |
|
50 | 60 | -10 |  |
| grand
icosidodécaèdre adouci
U57 découvert par Coxeter |
mêmes sommets qu'un pseudo rhombicosidodécaèdre | 5/2.34
(|2 5/2 3) |
92 | 60 | -8 |  |
| petit
dodécaèdre tronqué étoilé
U58 |
mêmes sommets que le rhombicosidodécaèdre | 10/3.5.10/3
(2 5|5/3) |
24 | 60 | -6 |  |
| dodécadodécaèdre
tronqué
U59 |
mêmes sommets qu'un pseudo icosidodécaèdre tronqué | 10/3.4.10
(5/3 2 5|) |
54 | 120 | -6 | 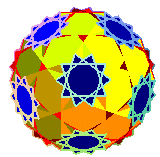 |
| dodécadodécaèdre
adouci inversé
U60 découvert par Coxeter |
mêmes sommets qu'un pseudo rhombicosidodécaèdre | 5/2.32.5.3
(|5/2 2 5) |
84 | 60 | -6 | 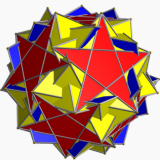 |
| grand
dodécicosidodécaèdre
U61 |
mêmes sommets que le grand dodécaèdre tronqué | 5/2.10/3.3.10/3
(5/2 3|5/3) |
42 | 60 | -16 |  |
| petit
dodécahémicosaèdre
U62 |
mêmes sommets que l'icosidodécaèdre | (6.5/2)2
(5/3 5/2|3) |
22 | 30 | -8 |  |
| grand
dodécicosaèdre
U63 |
mêmes sommets que le dodécaèdre tronqué | (6.10/3)2
3 5/3 (3/2 5/2) | ?? |
32 | 60 | -28 |  |
| grand
dodécicosidodécaèdre adouci
U64 découvert par Coxeter |
mêmes sommets qu'un pseudo rhombicosidodécaèdre | 5/2.3.5/2.33
(|5/2 5/2 3) |
104 | 60 | -16 |  |
| grand
dodécahémicosaèdre
U65 |
mêmes sommets que l'icosidodécaèdre | (5.6)2
(5 5|3) |
22 | 30 | -8 |  |
| grand
dodécaèdre tronqué étoilé
U66 découvert par Pitsch |
mêmes sommets que le petit icosicosidodécaèdre | 10/2.3.10/3
(2 3|5/3) |
32 | 60 | 2 |  |
| grand
rhombicosidodécaèdre
U67 |
mêmes sommets que le grand dodécaèdre tronqué | 5/2.4.3.4
(5/2 3|2) |
62 | 60 | 2 |  |
| grand
icosidodécaèdre tronqué
U68 |
mêmes sommets que l'icosidodécaèdre tronqué | 10/3.4.6
(5/3 2 3|) |
62 | 120 | 2 |  |
| grand
icosidodécaèdre adouci inversé
U69 découvert par Coxeter |
5/2.34
(|5/2 2 3) |
112 | 60 | -8 |  |
|
| grand
dodécahémidodécaèdre
U70 |
mêmes sommets que l'icosidodécaèdre | (5/2.10/3)2
(5/2 5/2|5/3) |
18 | 30 | -12 |  |
| grand
icosihémidodécaèdre
U71 |
mêmes sommets que l'icosidodécaèdre | (3.10/3)2
(3 3|5/3) |
26 | 30 | -4 |  |
| petit
icosicosidodécaèdre rétroadouci
U72 découvert par Coxeter |
(5/2.35)/2
(|3 3 5/2) |
112 | 60 | -8 |  |
|
| grand
rhombidodécaèdre
U73 |
mêmes sommets que le grand dodécaèdre tronqué | 4.10/3.4.10/3
2 5/3 (3/2 5/4) |?? |
42 | 60 | -18 |  |
| grand
icosidodécaèdre rétroadouci
U74 découvert par Coxeter |
(34.5/2)/2
(|3 5/2 2) |
92 | 60 | -28 |  |
|
| grand
dirhombicosidodécaèdre
U75 découvert par Coxeter |
mêmes sommets qu'un pseudo rhombicosidodécaèdre | 4.5/2.4.3.4.5/2.4.3
(|3/2 5/3 3 5/2) |
124 | 60 | -56 |  |
Il existe un 43-ième "polyèdre" de ce type,
appelé grand
dirhombidodécaèdre disadouci, ou polyèdre de Skilling,
si on accepte que des paires d'arêtes coïncident.
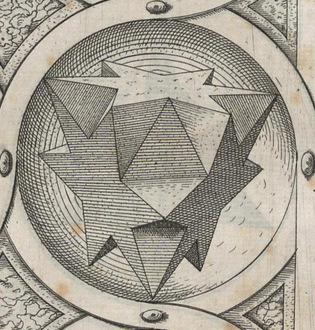
| L'orfèvre Wentzel Jamnitzer a publié en
1568 un ouvrage, Perspectiva
corporum regularium, dans lequel se trouvent une multitudes de gravures
représentant des variations autour des polyèdres réguliers.
Par exemple ce tétraèdre tronqué où les faces hexagonales sont remplacées par des étoiles à 6 branches. Malgré les similitudes avec les polyèdres de Badoureau, les hexagones étoilés ne sont pas des polygones simples, donc cet élégant objet ne peut qu'être considéré comme un polyèdre à 20 faces non convexes, et non régulières... |
 |
 |
| polyèdre suivant | polyèdre précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2014