Famille	polyèdre étoilé semi-régulier (ou uniforme U75), ou polyèdre de Badoureau Coxeter (inconnu de Badoureau, n'a été découvert qu'en 1932 par Coxeter et Miller)
Étymologie	di + icosi car il y a 2.20 faces triangulaires, di + dodéca car il y a 2.12 faces pentagonales, et rhombi car il y a des faces carrées.
Historique	Découvert par Miller et Coxeter en 1954 ; d'où l'autre appellation : monstre de Miller
Dual
Faces	40 triangles, 60 carrés et 24 pentagones étoilés
Sommets	60 sommets , de code de Schläfli 4.5/2.4.3.4.5/2.4.3 (seul polyèdre étoilé semi-régulier à avoir des sommets de degré > 6)
Arêtes	60 arêtes
Coordonnées de sommets	et les permutés circulaires  (un groupe de 12 points et deux groupes de 24)
Groupe des isométries	celui du dodécaèdre

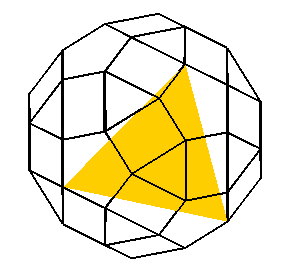
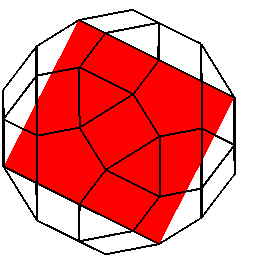
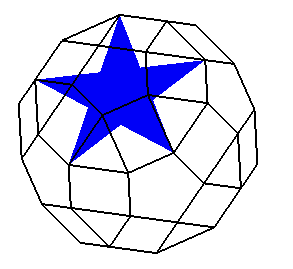
L'enveloppe convexe des sommets du grand dirhombicosidodécaèdre fournit un polyèdre équivalent au rhombicosidodécaèdre, mais dont les faces carrées sont allongées en des rectangles.

Ci-dessous, vue de l'insertion de chaque type de face dans cette enveloppe convexe.
 

© Robert FERRÉOL 2008