|
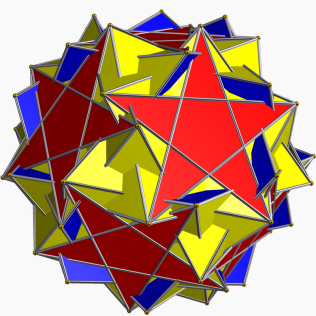
grand icosidodécaèdre adouci |
dodécadodécaèdre adouci inversé |
grand dodécicosidodécaèdre adouci |
| Famille |
polyèdre étoilé
semi-régulier (ou uniforme U57), ou polyèdre
de Badoureau Coxeter (inconnu de Badoureau, n'a été découvert
qu'en 1932 par Coxeter et Miller) |
Idem, U60 |
Idem, U64 |
| Faces |
80 triangles et 12 pentagones étoilés |
60 triangles, 12 pentagones et 12 pentagones étoilés |
80 triangles, 24 pentagones étoilés |
| Sommets |
60 sommets, de code
de Schläfli 5/2.34 |
60 sommets, de code
de Schläfli 3.5/2.32.5 |
60 sommets, de code
de Schläfli 5/2.3.5/2.33 |
| Arêtes |
150 arêtes |
150 arêtes |
180 arêtes |
| Construction |
|
12 pentagones étoilés aux sommets d'un
icosaèdre régulier superposés à 12 pentagones
non étoilés, et 60 triangles joignant un côté
d'un pentagone à un des sommets d'un autre. |
|
| Groupe des isométries |
celui du dodécaèdre |
Idem |
Idem |
| Remarque |
|
|
Ce polyèdre la particularité de possèder
des faces coplanaires (forcément non contigües) |