Autre nom : polyèdre ou solide Archimédien. Archimède de Syracuse (287-212 av. J.C.) : savant grec. www.srcf.ucam.org/~rjw62/polyhedra/entry/archimedeansolids.html APMEP 486 p. 60

Les polyèdres d'Archimède sont les 13 polyèdres semi-réguliers autres que les polyèdres réguliers, les prismes et les antiprismes.

On peut les caractériser par le code de Schläfli commun aux sommets, qui indique, dans l'ordre, les types de polygones réguliers que reçoit chaque sommet.
Par exemple : 3.5².4 signifie que chaque sommet reçoit un triangle, puis deux pentagones, et un carré.
 

Le premier de ces polyèdres d'Archimède possède les symétries du tétraèdre :
 

Nom officiel	construction	code de Schläfli	faces	nombre de sommets	figure
tétraèdre tronqué	tétraèdre faiblement tronqué	3.62	4 triangles 4 hexagones	12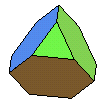

Les 12 autres se répartissent en deux classes de 6 polyèdres, la première possédant les symétries du cube et de l'octaèdre, la deuxième celles du dodécaèdre et de l'icosaèdre.

Les deux derniers polyèdres du tableau ci-dessous, obtenus par adoucissement, ne sont pas énantiomorphes (c'est-à dire équivalents à leur image miroir), c'est pourquoi certains comptent 15 polyèdres d'Archimède différents au lieu de 13.
 
 

nom officiel	construction	code de Schläfli	figure	nom officiel	construction	code de Schläfli	figure
cube tronqué	cube faiblement tronqué	3.82		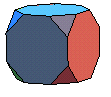dodécaèdre tronqué	dodécaèdre faiblement tronqué	3.102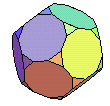
octaèdre tronqué	octaèdre faiblement tronqué	4.62		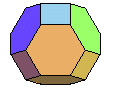icosaèdre tronqué	icosaèdre faiblement tronqué	5.62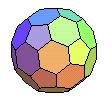
cuboctaèdre	cube (ou octaèdre) fortement tronqué	(3.4)2		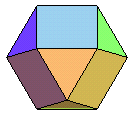icosidodécaèdre	dodécaèdre (ou icosaèdre) fortement tronqué	(3.5)2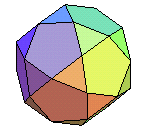
rhombicuboctaèdre	cube (ou octaèdre) chanfreiné	3.43		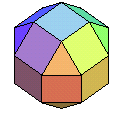rhombicosidodécaèdre	dodécaèdre (ou icosaèdre) chanfreiné	3.4.5.4
cuboctaèdre tronqué	cube (ou octaèdre) tronqué aux arêtes et fortement tronqué aux sommets	4.6.8		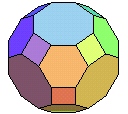icosidodécaèdre tronqué	dodécaèdre (ou icosaèdre) tronqué aux arêtes et fortement tronqué aux sommets	4.6.10
cube adouci	cube (ou octaèdre) adouci	34.4		dodécaèdre adouci	dodécaèdre (ou icosaèdre) adouci	34.5

Formule de Guy Le Berre : si  est la somme des angles en radian arrivant en un sommet, le nombre de sommets du polyèdre semi-régulier est donné par .

Voir aussi les polyèdres de Catalan, duaux des archimédiens.

Aux 13 polyèdres d'Archimède correspondent 13 pavages de la sphère par des polygones sphériques réguliers bord à bord dont le groupe des isométries agit transitivement sur les sommets. Nous les relions ci-dessous à 7 des 8 pavages du plan par des polygones réguliers ayant des propriétés similaires, dits pavages "semi-réguliers" (dont la définition peut juste consister à dire que les polygones sont réguliers à arêtes jointives et que tous les sommets sont identiques).
 

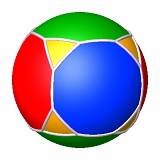
Tout d'abord, les 5 pavages sphériques associés aux troncatures faibles des 5 polyèdres réguliers (images réalisées par Alain Esculier) :

tétraèdre tronqué 3.62	cube tronqué 3.82	octaèdre tronqué 4.62	dodécaèdre tronqué 3.102	icosaèdre tronqué 5.62

sont à relier aux troncatures faibles de 2 des 3 pavages réguliers (la troncature faible du pavage triangulaire redonnant le pavage hexagonal):

pavage carré (ou quadrillage) tronqué 4.82	pavage hexagonal (ou hexillage) tronqué  3.122

 

Les deux pavages sphériques obtenus par troncature forte :			sont à relier au pavage plan obtenu de la même manière (la troncature forte du quadrillage redonnant un quadrillage) :
	cube (ou octaèdre) fortement tronqué, cuboctaèdre (3.4)2	dodécaèdre (ou icosaèdre) fortement tronqué, icosidodécaèdre (3.5)2		hexillage (ou deltillage) fortement tronqué, pavage trihexagonal ou hexadeltillage (3.6)2

les deux pavages sphériques obtenus par chanfreinage :			sont à relier au pavage plan obtenu de la même manière (le chanfreinage du quadrillage redonnant un quadrillage) :
	cube (ou octaèdre) chanfreiné, rhombicuboctaèdre 3.43	dodécaèdre (ou icosaèdre) chanfreiné, rhombicosidodécaèdre 3.4.5.4		hexillage (ou deltillage) chanfreiné, rhombihexadeltillage 3.4.6.4, ou "pavage de Diane"

les deux pavages sphériques obtenus par troncature des arêtes et forte troncature des sommets :			sont à relier au pavage plan obtenu de la même manière :
	cuboctaèdre tronqué 4.6.8	icosidodécaèdre tronqué 4.6.10		hexadeltillage tronqué 4.6.12

 

les deux pavages sphériques obtenus par adoucissement			sont à relier aux 2 pavages plans obtenus par la même méthode :
	cube (ou octaèdre) adouci 34.4	dodécaèdre (ou icosaèdre) adouci 34.5		quadrillage adouci 32.4.3.4 dual du pavage du Caire	hexillage adouci 34.6

Ces 7 pavages sont aussi appelés "pavages d'Archimède".
 

Il existe un huitième pavage semi-régulier, plutôt apparenté aux antiprismes, appelé "quadrillage iso-adouci", de code 33.42.	Comme pour le rhombicuboctaèdre, on peut tourner d'un huitième de tour certains octogones du pavage de Diane, mais contrairement au gyro-rhombicuboctaèdre, les sommets ne sont plus tous du même type.

 
 

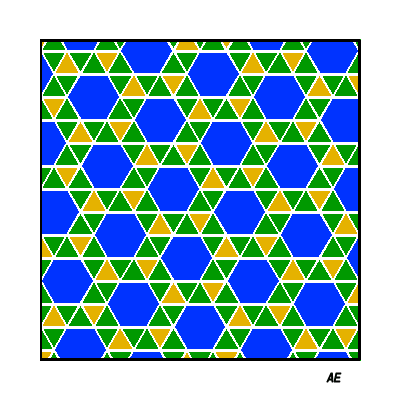
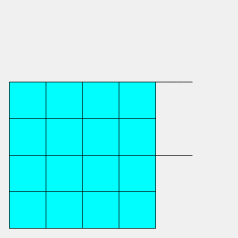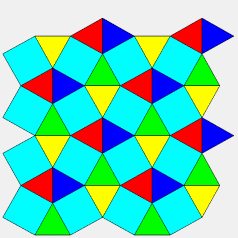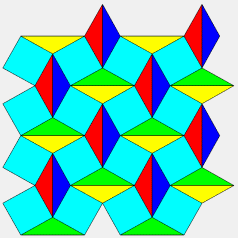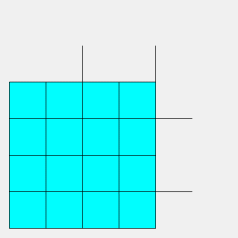
Figure montrant en quoi le 32.4.3.4 est un quadrillage adouci. Chaque arête d'un quadrillage bleu est remplacée par deux triangles verts, et, aux sommets, apparaissent des carrés jaunes.	Idem pour l'hexillage adouci 34.6, qui est aussi un deltillage adouci.
Animation montrant la construction par un mécanisme de carrés articulés, en partant du pavage carré.	Ici, animation de la construction par des hexagones et triangles articulés, en partant du pavage hexagonal tronqué. La position finale est le pavage de Diane.

Autre coloration des deux pavages du type "adouci".

 

Le quadrillage tronqué est très apprécié des carreleurs, avec parfois des octogones pas tout à fait réguliers (à gauche), ou des variantes (à droite, deux quadrillages tronqués superposés).
Deux pavages vus au musée juif de Prague. A gauche, un quadrillage tronqué dont les octogones ont été séparés en 8 triangles. A droite, superbe entrelacs construit sur un pavage trihexagonal.
Par projection gnomonique sur la sphère, puis projection stéréographique sur le plan, voici ce que devient (à gauche) le pavage trihexagonal (réalisation : Guy Valette).  A doite, image d'un "kagome", tissage de bambou  traditionnel japonais qui donne le même entrelacs que ci-dessus. Son nom est composé des mots "kago", qui signifie "panier", et "me", qui signifie "œil ".

 

polyèdre suivant

polyèdre précédent

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2015