Polyèdre adouci

POLYÈDRE ADOUCI
Snub polyhedron, abgeschrägtes Polyeder

Autre nom : polyèdre camus.
cf. xavier.hubaut.info/coursmath/pol/snub.htm
Programme d'adoucissement des polyèdres donnant les figures de cette page réalisé par Alain Esculier.

Un polyèdre adouci est un polyèdre obtenu en remplaçant dans le polyèdre de départ les arêtes par une suite de faces, de sorte à "adoucir" les angles entre les faces.

Plus précisément, chaque sommet de degré d est remplacé par un polygone d'ordre d (en bleu ci-contre), et chaque arête par 2 triangles (en vert). Les faces issues des anciennes faces (en jaune) restent du même ordre.

Si le polyèdre de départ a F₀ faces, S₀ sommets de degrés d_i et A₀ arêtes, un polyèdre adouci a alors :
S = somme(d_i) sommets
F = F₀ + S₀ + 2 A₀ faces
A = somme(d_i) + 3A₀ arêtes

Un polyèdre adouci d'un dual est équivalent au polyèdre de départ.

Les cinq polyèdres réguliers possèdent chacun un polyèdre adouci qui est semi-régulier, obtenu en transformant chaque face par une similitude de centre le centre de la face, d'angle q et de rapport k déterminés de sorte que les triangles verts soient équilatéraux ; voici les 3 exemples :

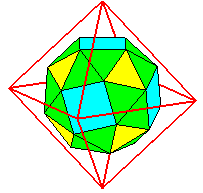
Le cube adouci, qui est aussi (à réflexion près) l'octaèdre adouci.
Les 6 faces carrées correspondent aux 6 faces du cube (ou aux 6 sommets de l'octaèdre), les 8 triangles bleus correspondent aux 8 sommets du cube (ou les 8 triangles jaines aux 8 faces de l'octaèdre), et les 24=2.12 triangles verts correspondent aux 12 arêtes du cube ou de l'octaèdre.

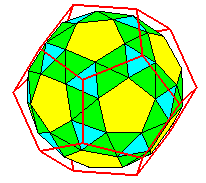
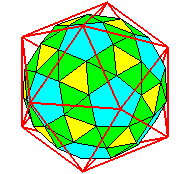
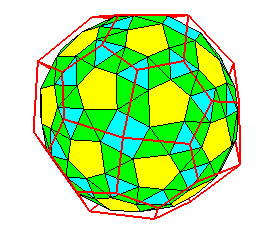
Le dodécaèdre adouci, qui est aussi l'icosaèdre adouci.
Les 12 faces pentagonales correspondent aux 12 faces du dodécaèdre (ou aux 12 sommets de l'icosaèdre), les 20 triangles bleus correspondent aux 20 sommets du dodécaèdre (ou les 20 triangles jaunes aux 20 faces de l'icosaèdre), et les 60=2.30 triangles verts correspondant aux 60 arêtes du dodécaèdre ou de l'icosaèdre.

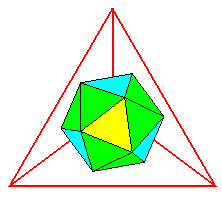
Le tétraèdre adouci :
4 faces triangulaires jaunes comme le tétraèdre plus 4 triangles bleus correspondant aux sommets du tétraèdre, plus 12= 2.6 triangles verts correspondant aux arêtes ; ce n'est autre que l'icosaèdre !

Autres exemples :

Icositétraèdre pentagonal adouci
Pentaki-dodécaèdre adouci
Dodécaèdre rhombique adouci

Voir aussi le chanfreinage et les pavages adoucis.

polyèdre suivant polyèdre précédent courbes 2D courbes 3D surfaces fractals polyèdres

Le cube adouci, qui est aussi (à réflexion près) l'octaèdre adouci. Les 6 faces carrées correspondent aux 6 faces du cube (ou aux 6 sommets de l'octaèdre), les 8 triangles bleus correspondent aux 8 sommets du cube (ou les 8 triangles jaines aux 8 faces de l'octaèdre), et les 24=2.12 triangles verts correspondent aux 12 arêtes du cube ou de l'octaèdre.
Le dodécaèdre adouci, qui est aussi l'icosaèdre adouci. Les 12 faces pentagonales correspondent aux 12 faces du dodécaèdre (ou aux 12 sommets de l'icosaèdre), les 20 triangles bleus correspondent aux 20 sommets du dodécaèdre (ou les 20 triangles jaunes aux 20 faces de l'icosaèdre), et les 60=2.30 triangles verts correspondant aux 60 arêtes du dodécaèdre ou de l'icosaèdre.
Le tétraèdre adouci : 4 faces triangulaires jaunes comme le tétraèdre plus 4 triangles bleus correspondant aux sommets du tétraèdre, plus 12= 2.6 triangles verts correspondant aux arêtes ; ce n'est autre que l'icosaèdre !