ayant
un angle de 
à côtés égaux, les quatre autres angles étant
égaux (à 
)
et les 3 autres côtés également égaux, où
t
est
la constante
de Tribonacci, unique racine réelle de 
.
.
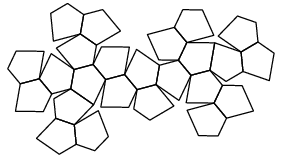
sphère circonscrite
aire : 
.
coefficient isopérimétrique :
.| polyèdre suivant | polyèdre précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
ICOSITÉTRAÈDRE PENTAGONAL
Pentagonal icositetrahedron, Pentagonikositetraeder
| Famille | polyèdre semi-régulier de deuxième espèce |
| Historique | étudié par Catalan en 1862 |
| Étymologie | icositétra = 24 ; les faces sont des pentagones. |
| Dual | cube adouci |
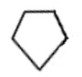
| Faces | 24 pentagones ayant
un angle de
à côtés égaux, les quatre autres angles étant
égaux (à )
et les 3 autres côtés également égaux, où
t
est
la constante
de Tribonacci, unique racine réelle de . |
| Sommets | 38, dont 32 de degré 3, de code de Schläfli 53 et 6 de degré 4 de code 54. |
| Arêtes | 60, dont 24 de longueur a et 36 de longueur . |
| Patron et graphe |
|
| Diamètres | sphère inscrite : 2,74
a
;
sphère circonscrite |
| Mensurations | volume :
aire : .
coefficient isopérimétrique : . |
| Construction | Dual polaire du cube adouci. |
| Particularité | chiral (non égal à son image miroir) |
| Groupe des isométries | = groupe des rotations du cube ou de l'octaèdre (pas d'isométrie négative). |
Pour ne pas les confondre : icositétraèdres
pentagonal, et trapézoïdal :
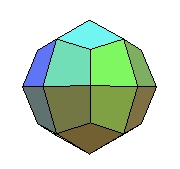
Icositétraèdre pentagonal adouci,
par Alain Esculier.
| polyèdre suivant | polyèdre précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2007