dodécadodécaèdre icositronqué  (ou icosidodécaèdre icosidodécatronqué)	dodécadodécaèdre tronqué  (ou dodécaèdre quasitronqué)
Famille	polyèdre étoilé semi-régulier (ou uniforme U45), ou polyèdre de Badoureau	idem, U59
Étymologie	dodécadodéca car il y a deux groupes de douze faces pentagonales ????	???
Dual
Faces	20 hexagones, 12 décagones et 12 décagones étoilés	30 carrés, 12 décagones et 12 décagones étoilés
Sommets	120 sommets, de code de Schläfli 6.10.10/3	120 sommets, de code de Schläfli 4.10.10/3
Arêtes	180 arêtes	idem
Construction
Coordonnées des sommets	et leurs permuté circulaires où  est le nombre d'or.	(Source : Wikipedia)
Groupe des isométries	celui du dodécaèdre	idem

 

L'enveloppe convexe des sommets fournit dans les deux cas un polyèdre équivalent à l'icosidodécaèdre tronqué, mais dont les faces hexagonales et quadrilatérales ne sont pas régulières. Cf. aussi le grand icosidodécaèdre tronqué.

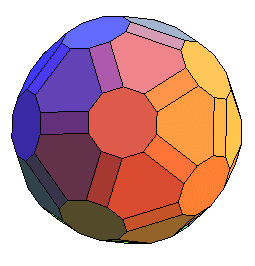
enveloppe convexe des sommets de U45

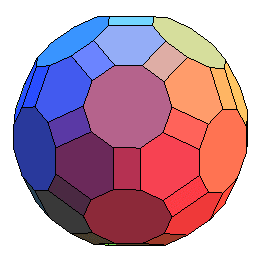
enveloppe convexe des sommets de U59

Ci-dessous, vue de l'insertion de chaque type de face dans cette enveloppe convexe.
 

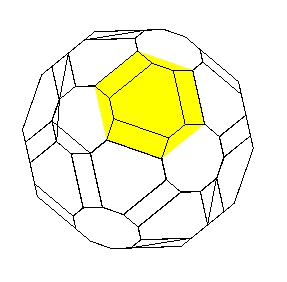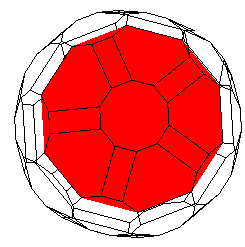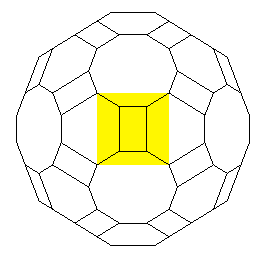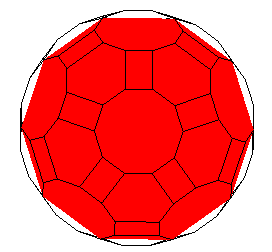Voir ici leurs cousins à symétrie cubique.
 

polyèdre suivant

polyèdre précédent

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2008