polyèdre suivant polyèdre précédent courbes 2D courbes 3D surfaces fractals polyèdres

GRAND ICOSAÈDRE
Great icosahedron, großes Ikosaeder

Famille polyèdre étoilé régulier, ou polyèdre de Képler-Poinsot
Historique découvert par Poinsot en 1809, avec son cousin le grand dodécaèdre
Etymologie "icosaèdre" car c'est un polyèdre à 20 faces ; ses 20 sommets sont aussi ceux de l'icosaèdre régulier.
Dual grand dodécaèdre étoilé
Faces 20 triangles
Sommets 12 sommets de degré 5, de code de Schläfli  35  ou mieux : 35/2 pour indiquer que les 5 triangles se croisent (la section d'un sommet donne un pentagone croisé) 
Arêtes 30 arêtes de longueur a 
Caractéristique
d'Euler-Poincaré		  =2  donc genre 0
Graphe des arêtes  le même que celui de l'icosaèdre régulier
Coordonnées 
des sommets		 cf. celles des sommets de l'icosaèdre régulier.
Construction

30 triangles inscrits dans l'icosaèdre

Squelette de l'icosaèdre avec l'une des faces du grand icosaèdre.
polyèdres dérivés par troncature forte : grand icosidodécaèdre
par troncature faible : grand icosaèdre tronqué

 
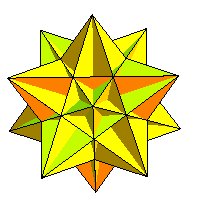
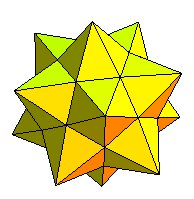
Le grand icosaèdre (à gauche) a les mêmes arêtes que le petit dodécaèdre étoilé de Képler (à droite).

 
polyèdre suivant polyèdre précédent courbes 2D courbes 3D surfaces fractals polyèdres

© Robert FERRÉOL 2014