Polyèdres de Képler découverts par ... Képler en 1619 ; polyèdres de Poinsot découverts par... Poinsot en 1809. Preuve que ce sont les seuls polyèdres réguliers étoilés par Cauchy en 1811. Sites : cage.rug.ac.be/~hs/polyhedra/keplerpoinsot.html

Les polyèdres de Képler-Poinsot sont les polyèdres étoilés réguliers.
Trois d'entre eux ont les mêmes sommets que l'icosaèdre régulier et le quatrième les mêmes que ceux du dodécaèdre régulier.

Les polyèdres de Képler, dont les faces sont elles-mêmes étoilées :
 

nom	Code de Schläfli	faces	sommets	arêtes	remarque	figure
petit dodécaèdre étoilé	(5/2)5	12 étoiles à 5 branches	12	30	dual du grand dodécaèdre
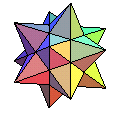
grand dodécaèdre étoilé	(5/2)3	12 étoiles à 5 branches	20	30	dual du grand icosaèdre

Les polyèdres de Poinsot, dont les faces sont des polygones convexes :
 

nom	Code de Schläfli	faces	sommets	arêtes	remarque	figure
grand dodécaèdre	55	12 pentagones	12	30	dual du petit dodécaèdre étoilé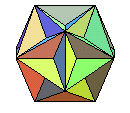
grand icosaèdre	53	20 triangles	12	30	dual du grand dodécaèdre étoilé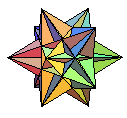

Voir aussi les polyèdres de Badoureau-Coxeter, étoilés semi-réguliers, les 10 polytopes étoilés réguliers en dimension 4, qui ne sont pas encore dans ce site (il n'en existe plus en dimension supérieure à 4), et les pavages étoilés.
 

polyèdre suivant

polyèdre précédent

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2017