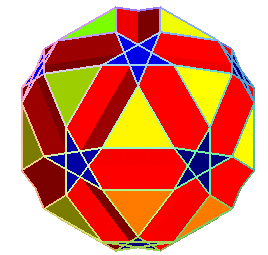
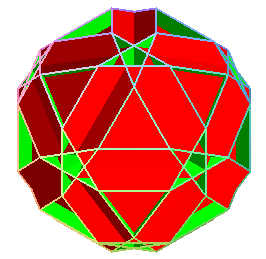
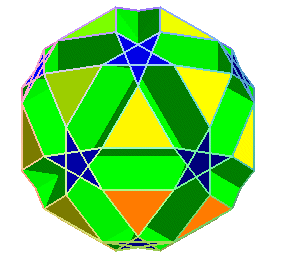
petit icosicosidodécaèdre	petit dodécicosaèdre	petit dodécicosidodécaèdre ditrigonal
Famille	polyèdre étoilé semi-régulier (ou uniforme U31), ou polyèdre de Badoureau	Idem, U50 (inconnu de Badoureau, n'a été découvert qu'en 1954 par Coxeter)	Idem, U43, également découvert par Coxeter.
Étymologie	icosicosi car il y a 2 groupes de 20 faces (triangulaires et hexagonales), dodéca car il y a 12 faces pentagonales et petit pour le différencier du grand	dodéc car il y a 12 faces décagonales, icosa car il y a 20 faces hexagonales et petit pour le différencier du grand	dodéc car il y a 12 faces pentagonales, icosi car il y a 20 faces triangulaires, dodéca car il y a 12 faces décagonales, ditrigonal (voir ci-dessous) et petit pour le différencier du grand
Dual
faces	20 triangles, 12 pentagones étoilés et 20 hexagones	20 hexagones et 12 décagones	20 triangles, 12 pentagones étoilés et 12 décagones
Sommets	60 sommets, de code de Schläfli 6.5/2.6.3	60 sommets, de code de Schläfli 6.10.6.10	60 sommets, de code de Schläfli 3.10.5/2.10
Arêtes	120 arêtes	Idem	Idem
Construction
Groupe des isométries	celui du dodécaèdre	Idem	Idem

Explication d'Alain lassine pour le ditrigonal : Je pense que c’est  parce que l’on peut construire 6 pyramides ditrigonales en utilisant les mêmes arêtes que ce polyèdre. Une pyramide ditrigonale étant une pyramide à base hexagonale, cet hexagone se reproduisant quand on lui applique une rotation de 120 degré. (Donc ayant 2 x 3 angles égaux d’où le di-tri-gonal).
 

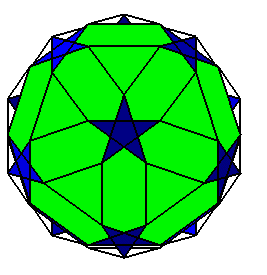
les faces pentagonales avec une face décagonale

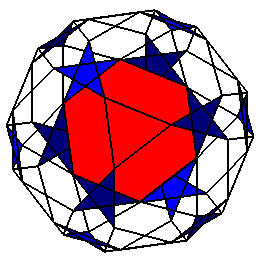
les faces pentagonales avec une face hexagonale

les faces pentagonales seules

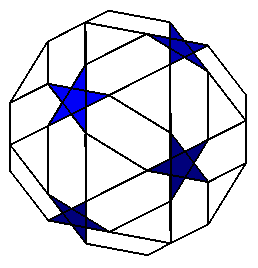
L'enveloppe convexe des sommets de ces trois polyèdres fournit un polyèdre équivalent au rhombicosidodécaèdre, avec des faces rectangulaires au lieu de carrées.

Voir aussi le grand dodécaèdre tronqué étoilé, qui a les mêmes sommets.
 

polyèdre suivant

polyèdre précédent

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2008