Tétrahémihexaèdre

TÉTRAHÉMIHEXAÈDRE
Tetrahemihexahedron, Tetrahemihexaeder

Famille	polyèdre étoilé semi-régulier (ou uniforme U4), ou polyèdre de Badoureau
Etymologie	tétra car il y a 4 faces triangulaires et hemihexa car il y a 6/2 faces carrées
Autres noms	heptaèdre de Reinhardt (du nom de Curt Reinhardt, qui a conçu ce polyèdre en 1885) hémicuboctaèdre (car il a moitié moins de faces que le cuboctaèdre et d'ailleurs aussi moitié moins de sommets et moitié moins d'arêtes)
Dual
faces	4 triangles et 3 carrés qui se croisent deux à deux (seul polyèdre semi-régulier à avoir un nombre impair de faces)
Sommets	6 sommets , de code de Schläfli 3.4.3.4
Arêtes	12 arêtes
Construction	cf. l'octaèdre, qui a les mêmes sommets et les mêmes arêtes.
Groupe des isométries	celui du tétraèdre (et non celui de l'octaèdre ; il n'y a pas les rotations d'un quart de tour par exemple)

Le tétrahémihexaèdre a pour caractéristique d'Euler-Poincaré 7 + 6 – 12 = 1 : sa surface est un modèle du plan projectif réel.

Ci-contre, un ruban de Möbius tracé sur la surface du tétrahémihexaèdre, montrant que celle-ci est bien unilatère.

Le tétrahémihexaèdre a la même structure que la surface romaine, autre modèle du plan projectif.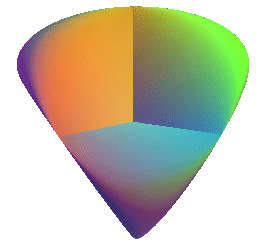

On obtient un revêtement à deux feuillets du tétrahémihexaèdre par troncature généralisée des arêtes et des sommets du tétraèdre (les 8 triangles et 6 rectangles de la troncature se recollent 2 à 2 pour former les 4 triangles et deux carrés du tétrahémihexaèdre).