PETIT CUBICUBOCTAÈDRE et PETIT RHOMBIHEXAÈDRE
Small cubicuboctahedron and small rhombihexahedron,
Kleines Kubikuboktaeder und kleines Rhombenhexaeder
| polyèdre suivant | polyèdre précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
PETIT CUBICUBOCTAÈDRE et PETIT RHOMBIHEXAÈDRE
Small cubicuboctahedron and small rhombihexahedron,
Kleines Kubikuboktaeder und kleines Rhombenhexaeder

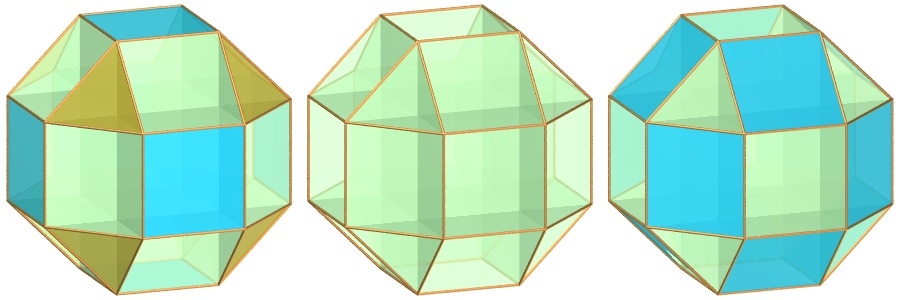
| petit cubicuboctaèdre | petit rhombihexaèdre | |
| Famille | polyèdre étoilé semi-régulier (ou uniforme U13), ou polyèdre de Badoureau. | idem, U18 |
| Etymologie | cubi car il y a 6 faces carrées, cub car il y a 6 faces octogonales et octa car il y a 8 faces triangulaires ; petit pour le différencier du grand. | rhombi car il y a des faces carrées et hexa car il y a 6 faces octogonales ; petit pour le différencier du grand. |
| Dual | ||
| faces | 8 triangles et 6 carrés et 6 octogones | 12 carrés et 6 octogones |
| Sommets | 24 sommets , de code de Schläfli 8.3.8.4 | 12 sommets, de code de Schläfli 8.4.8.4 |
| Arêtes | 48 arêtes | idem |
| Construction | cf. celle du rhombicuboctaèdre, qui a les mêmes sommets et les mêmes arêtes. | idem |
| Groupe des isométries | celui de l'octaèdre | idem |
Le petit cubicuboctaèdre a pour caractéristique d'Euler-Poincaré 20 + 24 - 48 = -4 et sa surface est orientable (donc équivalente au tore à 3 trous).
Le petit rhombihexaèdre a, lui, pour caractéristique
d'Euler-Poincaré 18 + 24 - 48 = -6 et sa surface est non orientable
(donc équivalente à la bouteille de Klein munie de 3 anses)

petit cubicuboctaèdre |

rhombicuboctaèdre |

petit rhombihexaèdre |

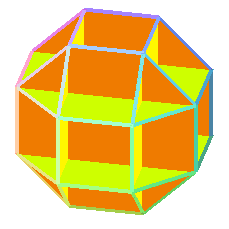

Ces deux polyèdres sont à la symétrie cubique ce que sont ceux-ci à la symétrie dodécaédrique.
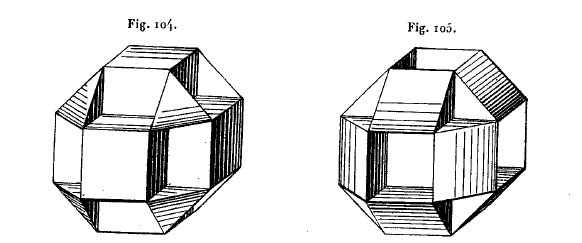
Ces deux polyèdres, dessinés par Badoureau en 1878.
| polyèdre suivant | polyèdre précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL
2008