polyèdre suivant polyèdre précédent courbes 2D courbes 3D surfaces fractals polyèdres

PETIT ICOSIDODÉCAÈDRE DITRIGONAL,
GRAND ICOSIDODÉCAÈDRE DITRIGONAL
et DODÉCADODÉCAÈDRE DITRIGONAL
Small ditrigonal icosidodecahedron,  great ditrigonal icosidodecahedron and ditrigonal dodecadodecahedron,
Kleines ditrigonales Ikosidodekaeder, grosses ditrigonales Ikosidodekaeder und ditrigonales Dodekadodekaeder

Image : Alain Esculier
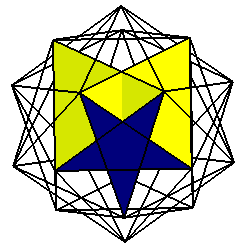
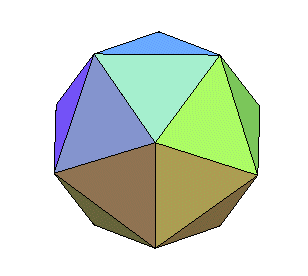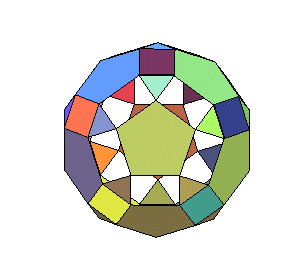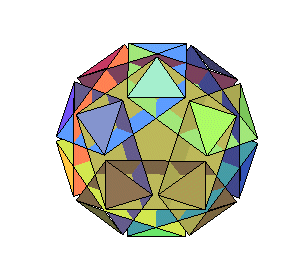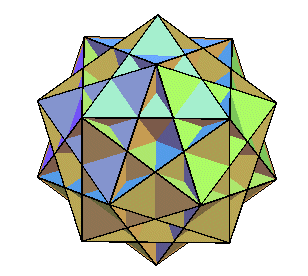
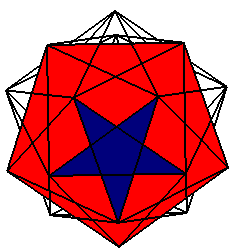
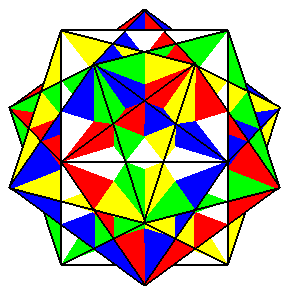
petit icosidodécaèdre ditrigonal grand  icosidodécaèdre ditrigonal dodécadodécaèdre ditrigonal
Famille polyèdre étoilé semi-régulier (ou uniforme U30), ou polyèdre de Badoureau. idem U47 idem U41
Étymologie icosi car il y a 20 faces triangulaires, dodéca car il y a 12 faces pentagonales ; petit pour le différencier du grand ci-contre ; ditrigonal car chaque sommet reçoit deux groupes de trois faces de même type. icosi car il y a 20 faces triangulaires, dodéca car il y a 12 faces pentagonales ; grand pour le différencier du petit ci-contre ; ditrigonal , idem. dodécadodéca car il y a 2 fois 12 faces pentagonales ; ditrigonal , idem.
Dual
faces 20 triangles et 12 pentagones étoilés 20 triangles et 12 pentagones 12 pentagones et 12 pentagones étoilés
Sommets 20 sommets , de code de Schläfli 5/2.3.5/2.3.5/2.3 20 sommets, de code de Schläfli  5.3.5.3.5.3 20 sommets, de code de Schläfli 5/2.5.5/2.5.5/2.5
Arêtes 60 arêtes  idem idem
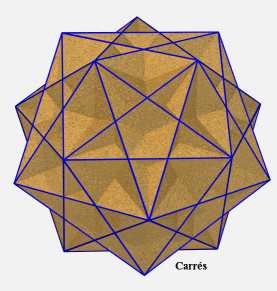
Construction les sommets sont ceux du dodécaèdre idem
mêmes sommets et arêtes que les deux autres !		 idem
Groupe des isométries celui du dodécaèdre idem idem

Le petit icosidodécaèdre ditrigonal a pour caractéristique d'Euler-Poincaré 32 + 20 - 60 = -8 et sa surface est orientable.

Le grand  icosidodécaèdre ditrigonal a pour caractéristique d'Euler-Poincaré 32 + 20 - 60 = -8 et sa surface est orientable .

Le dodécadodécaèdre ditrigonal a pour caractéristique d'Euler-Poincaré 24 + 20 - 60 = -16 et sa surface est orientable .

Ces 3 polyèdres montrent que le squelette d'un polyèdre n'est pas caractéristique du polyèdre.

Quelques vues des faces pentagonales étoilées

 

Un pentagone étoilé et deux triangles

un pentagone étoilé et un pentagone

 
polyèdre suivant polyèdre précédent courbes 2D courbes 3D surfaces fractals polyèdres

© Robert FERRÉOL 2008