TORE POLYÉDRIQUE PLAT
Flat polyedral Torus, Flacher Polyedertorus
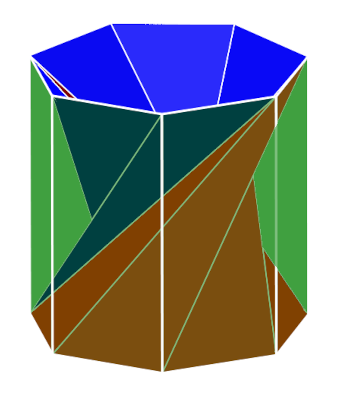
Cas n = 7
| polyèdre suivant | polyèdre précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
TORE POLYÉDRIQUE PLAT
Flat polyedral Torus, Flacher Polyedertorus

Cas n = 7
| Modèle transmis par Guy Valette, l'idée
revenant à Ulrich
Brehm en 1978.
Autre nom : diplotore. Voir ces pages : paper flat tori et diplotores-tores-polyedraux-plats. Vidéo de Henry Segermann ; figure interactive geogebra. |
Si 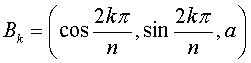 le tore polyédrique plat d'ordre n de Brehm est formé
des n faces triangulaires
le tore polyédrique plat d'ordre n de Brehm est formé
des n faces triangulaires |
Un polyèdre plat est un polyèdre
non convexe tel que la somme des angles des faces aboutissant à
chaque sommet est égale à 360° ; l'appellation plat
vient de ce que si un tel polyèdre était convexe, les faces
aboutissant à chaque sommet devraient être coplanaires (et
ce ne serait donc pas un polyèdre au sens classique).
| On remarquera que dans le polyèdre de Brehm, dont
les faces ne se croisent plus à partir de n = 7, les cinq
angles aboutissant à chaque sommet ont bien une somme de 360°,
car il y en a 3 qui sont les trois angles d'un même triangle à
isométrie près (les triangles En dépliant la figure des 5 faces aboutissant à un même sommet ci-contre, on obtient une figure plane. |
 |

|
Si l'on désigne par courbure d'un sommet
le nombre 360° moins la somme des angles des faces y aboutissant, on
montre que la somme des courbures des sommets est égale à
360° fois la caractéristique
d'Euler-Poincaré de la surface du polyèdre.
Un polyèdre plat doit donc avoir une caractéristique
d'Euler-Poincaré nulle, et ne peut donc qu'être toroïdal.
On a bien ici .
 |
En effectuant une rotation de la partie supérieure et en triangulant les faces latérale on obtient un polyèdre qui reste plat (idée d'Alain Esculier). |
| polyèdre suivant | polyèdre précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL Alain ESCULIER 2025