MONOÈDRE
Monohedron, Monoeder
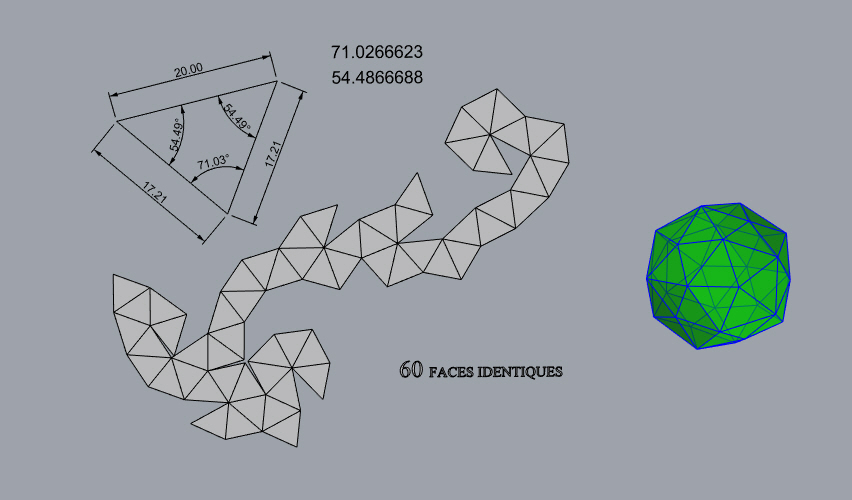
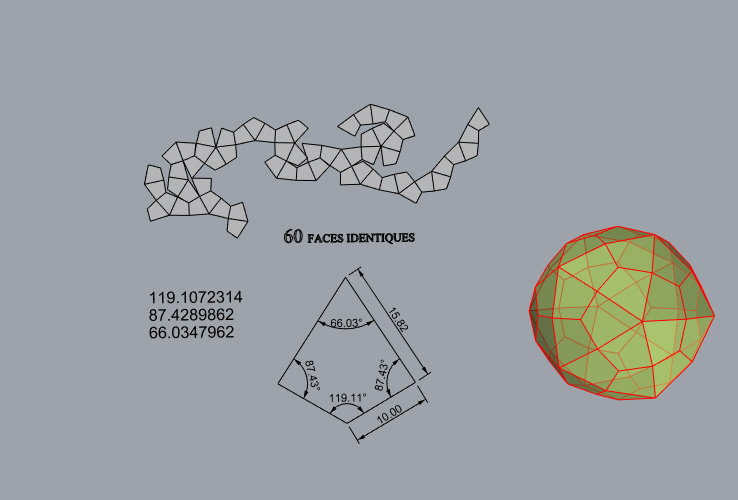
Deux exemples de monoèdres non isoèdres : intersection
des prismes construits sur les faces de l'icosaèdre (intersection
de 10 prismes hexagonaux), et intersection des prismes construits sur les
faces du dodécaèdre (intersection de 6 prismes décagonaux)
| Des préfixe et suffixe grecs mono- et -èdre. |
Le terme "monoèdre" désigne plusieurs concepts
différents.
1) En cristallographie, il désigne le plan,
"polyèdre" à une face.
2) Jean-Pierre
Petit a appelé "monoèdre" un rotoïde
à une arête et une face.
3) Branko
Grünbaum désigne par "monoèdre" ou "polyèdre
monoédrique" un (vrai) polyèdre dont toutes les faces
sont isométriques. Le terme d'étymologie latine équivalent
est "polyèdre équifacial", terme utlisé par exemple
pour le "tétraèdre
équifacial".
Cette définition s'étend aux pavages
monoédriques.
Attention : le terme "isoèdre" ou "polyèdre
isoédrique" désigne les polyèdres monoédriques
vérifiant la condition supplémentaire que leur groupe des
isométries agisse transitivement sur les faces : ce sont les polyèdres
semi-réguliers de seconde espèce.
© Robert FERRÉOL
Robert March, 2023

