DUAL D'UN POLYTOPE
Dual of a polytope, Dual eines Polytops
Si (P) est un polytope
de dimension n, notons 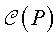 l'ensemble formé des ensembles des sommets de toutes les k-cellules
de (P), pour k allant de –1 à n (la –1-cellule
étant par convention l'ensemble vide) ;
l'ensemble formé des ensembles des sommets de toutes les k-cellules
de (P), pour k allant de –1 à n (la –1-cellule
étant par convention l'ensemble vide) ;
deux polytopes (P) et (P*) sont alors dits
combinatoirement
duaux s'il existe une dualité de 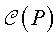 dans
dans 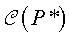 ,
c'est-à-dire une bijection envoyant les k-cellules de l'un
sur les (n – k –1) cellules de l'autre qui renverse les inclusions
(autrement dit, si C1 est une cellule de C2, elle-même cellule de
(P) , C2* est une cellule de C1* (l'existence d'une bijection conservant
les types de cellules et leurs inclusions signifiant l'équivalence
combinatoire des polytopes).
,
c'est-à-dire une bijection envoyant les k-cellules de l'un
sur les (n – k –1) cellules de l'autre qui renverse les inclusions
(autrement dit, si C1 est une cellule de C2, elle-même cellule de
(P) , C2* est une cellule de C1* (l'existence d'une bijection conservant
les types de cellules et leurs inclusions signifiant l'équivalence
combinatoire des polytopes).
Dans une dualité, les sommets de l'un des polytopes
corespondent donc aux hyperfaces de l'autre.
Un dual d'un dual est un polytope équivalent au
polytope de départ.
Par exemple, si (P) est un carré ABCD, 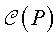 =
{ {}, {A},{B},{C},{D},{A,B},{B,C},{C,D},{D,A},{A,B,C,D}}, (P)
est auto-dual par la dualité définie par
=
{ {}, {A},{B},{C},{D},{A,B},{B,C},{C,D},{D,A},{A,B,C,D}}, (P)
est auto-dual par la dualité définie par 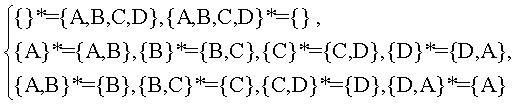
Exemples :
- les polygones sont auto-duaux
- voir la page spécifique des
duaux
des polyèdres, des polychores.
- l'hypertétraèdre
est auto-dual, le dual de l'hypercube
est le cocube.
© Robert FERRÉOL
2009