polyèdre suivant polyèdre précédent courbes 2D courbes 3D surfaces fractals polyèdres

HEXACONTAÈDRE PENTAGONAL
Pentagonal hexecontahedron, Pentagonhexakontaeder

Modèle réalisé avec Povray par Alain Esculier
Famille polyèdre semi-régulier de deuxième espèce
Historique étudié par Catalan en 1862
Étymologie hexaconta = 60 ; les faces sont des pentagones.
Dual dodécaèdre adouci
Faces 24 pentagones ayant un angle de 67° 28' à côtés égaux, les quatre autres angles étant égaux (à 118° 08' ) et les 3 autres côtés également égaux.
Angle dièdre: 153°10'
Sommets 92, dont 80 de degré 3, de code de Schläfli 53 et 12 de degré 5 de code 55.
Arêtes 150, dont 60 de longueur a et 90 de longueur 0,57a.
Patron et graphe
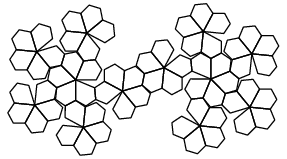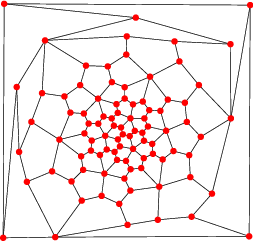Diamètres sphère inscrite :  4 a ; sphère circonscrite 
Mensurations volume : 35,43 a3  aire : 53,14a2 .
coefficient isopérimétrique : 0,95.
Construction Dual polaire du dodécaèdre adouci.
Particularité chiral (non égal à son image miroir)
Groupe des isométries  = groupe des rotations du dodécaèdre (pas d'isométrie négative).

Hexacontaèdre réalisé en carton par Robert March et ses élèves.

Hexacontaèdre pentagonal tronqué aux sommets.
La troncature des 12 sommets de degré 5 a fait apparaitre 12 pentagones, et les 24 pentagones sont devenus des hexagones.
Les 80 sommets de degré 3 sont restés et les 12 troncatures ont fait apparaitre 12.5 = 60 nouveaux sommets, donc il y a 140 sommets.

Modèle en bois réalisé par Roland Gagneux.

 
 
polyèdre suivant polyèdre précédent courbes 2D courbes 3D surfaces fractals polyèdres

© Robert FERRÉOL 2012