SURFACE DE BÉZIER
Bézier
surface, Béziersche Fläche
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
SURFACE DE BÉZIER
Bézier
surface, Béziersche Fläche
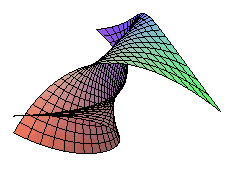
| Pierre Bézier (1910 - 1999) : ingénieur à la régie Renault. |
| Paramétrisation affine : Surface polynomiale de degré |
Des points
étant donnés (appelés points de contrôle), la
surface ou "carreau" de Bézier associée est la surface de
paramétrisation ci-dessus ; la portion de la surface pour u
et v
0 est incluse dans l'enveloppe convexe des points de contrôle.
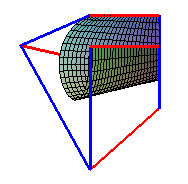
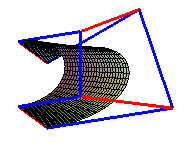
Exemple avec n = 1 et m = 3 (8 points de contrôle)
 |
 |
 |
Si l'on note
le point de paramètre t de la courbe
de Bézier de points de contrôle
,
et
le point de paramètre (u,v) de la surface de Bézier
de points de contrôle
,
l'on a la relation :
,
ce qui montre que la surface de Bézier est doublement une réunion
de courbes de Bézier.
Elle contient en particulier les 4 courbes de Bézier
de points de contrôles
,
,
et
.
Pour n = m = 1 (4 points de contrôle),
la surface de Bézier n'est autre que le paraboloïde
hyperbolique ayant pour génératrices les 4 droites
.

Les surfaces de Bézier sont des cas particuliers de surfaces splines.
Il existe une
autre sorte de surface de Bézier, définie par une triangulation
au lieu d'un "carrelage".
 |
 |
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL
2014