COURBE DE BÉZIER
Bezier
curve, BezierKurve
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
COURBE DE BÉZIER
Bezier
curve, BezierKurve
| Courbe étudiée par Pierre
Bézier en 1956 et, indépendamment, par Paul
de Casteljau en 1958.
Pierre Bézier (1910 - 1999) : ingénieur à la régie Renault. Regarder énoncé centrale PC 99. |
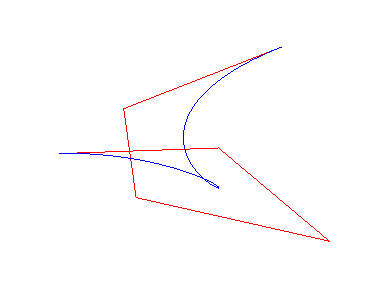
Paramétrisation affine : 
(soit  )
où les 
sont les polynômes de Bernstein :  .
Courbe algébrique polynomiale de degré £ n. Courbure en A0 :  . |
Une ligne brisée 
étant donnée (appelée polygone de contrôle,
les Ak étant les points
de contrôle), la courbe de Bézier (polynomiale) associée
est la courbe de paramétrisation ci-dessus ; la courbe passe par
A0
(pour t = 0) et An (pour
t
= 1), et la portion qui joint ces points est tracée dans l'enveloppe
convexe des points de contrôle ; la tangente en A0
est
(A0A1)
et celle en An (An-1An).
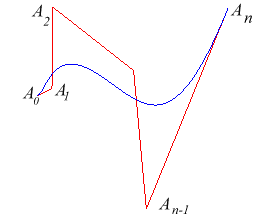
Construction récursive (algorithme de de Casteljau,
ingénieur chez Citroën) :
Le point 
est le barycentre de 
et 
où 
sont les points courants respectifs des courbes de Bézier de polygone
de contrôle 
et 
; de
plus la droite 
est la tangente en
à la courbe de Bézier.
Réciproquement, toute courbe algébrique
polynomiale
est une courbe de Bézier avec unicité du polygone de contrôle
associé, une fois les extrémités de ce polygone choisies
arbitrairement sur la courbe.
|
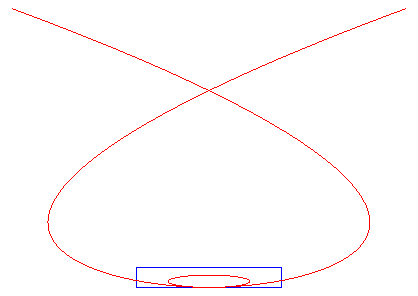
Voici un exemple de courbe de Bézier fermée avec sa courbe de contrôle en bleu. Est-ce un cercle ? Non ! Comme il y a 6 points de contrôles (avec A0 = A5), c'est une quintique , tracée à droite en (presque) totalité, avec aplatissement. Les points de contrôles sont (0,0),(1,0),(1,h)(-1,h),(-1,0),(0,0),
avec |
 |
 |
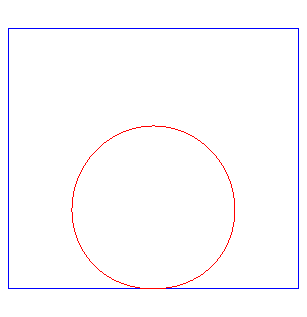
| En infographie, un cercle est souvent tracé de
façon approchée par 4 courbes de Bézier cubiques comme
celle ci-contre.
Les points de contrôles sont (1,0),(1,h)(h,1),(0,1), avec  ,
calculé de sorte que la courbe passe par  .
A droite, la cubique complétée, une parabole divergente à point double. |
 |
 |
 |
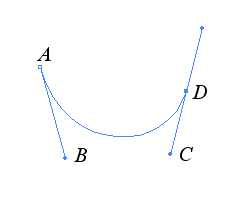Les courbes de bézier sont utilisées dans les logiciels de dessin comme illustrator, avec l'outil "pen tool" ; ci-contre cet outil à permis de tracer la courbe de Bézier cubique de polygône de contrôle ABCD. |
Les courbes de Bézier sont des cas particuliers
de courbes splines et se généralisent
en les courbes de
Bézier rationnelles.
Voir aussi les courbes
de Lagrange, les courbes
de Bézier 3D, les surfaces
de Bézier.
Regarder aussi :
demonstrations.wolfram.com/SimpleSplineCurves
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL
2000
,
calculé de sorte que les distances entre les points à tangentes
verticales et entre les points à tangentes horizontales soient égales.