Affine parametrization:  (i.e. ) where  are the Bernstein polynomials: . Polynomial algebraic curve of degree £ n. Curvature at A0 : .

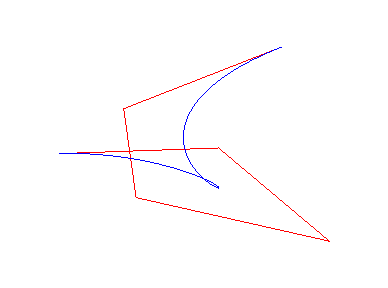
Given a broken line  (called control polygon, (A_k) being the control points), the associated (polynomial) Bezier curve is the curve with the aforementioned parametrization ; the curve passing through A₀ (for t = 0) and A_n (for t = 1) and has its portion joining these points traced in the convex envelope of the control points ; the tangent at A₀ is (A₀A₁) and the one at A_n is (A_n-1A_n).

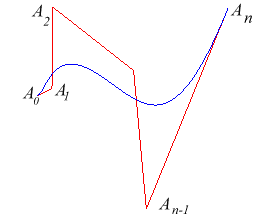
Recursive construction (algorithm invented by Casteljau, engineer for Citroën):
The point  is the barycentre of  and  where  are the current points respectively on the Bezier curves whose control polygons are  and  ; moreover, the line  is tangent in  to the Bezier curve.

Conversely, every polynomial algebraic curve is a Bezier curve with a one-to-one correspondence with the control polygon, once its extremities are chosen arbitrarily on the curve.

Here is an example of a closed Bezier curve and its control curve in red:

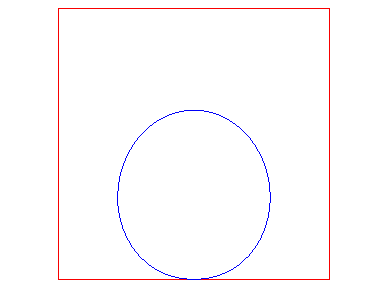
Is it a circle?

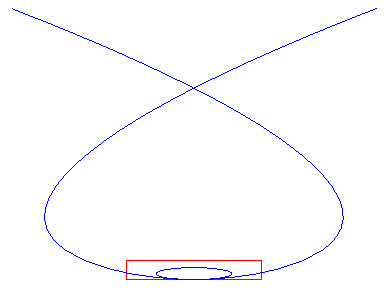
No! Since there are 6 control points (with A₀ = A₅), it is a quintic ; here is an (almost) complete flattened representation:

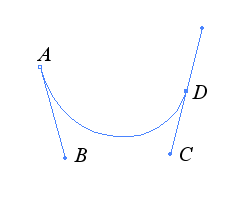Bezier curves are used in drawing software such as Illustrator, with the tool "pen tool"; on the left, the cubic Bezier curve with ABCD as control polygon was traced using this tool.

Bezier curves are examples of spline curves and can be generalized into rational Bezier curves.
See also Lagrange curves, 3D Bezier curves, Bezier surfaces.

Also look at:
demonstrations.wolfram.com/SimpleSplineCurves
 

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL  2017