BESACE
Besace,
Quersackkurve
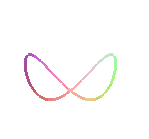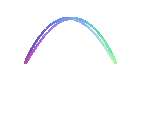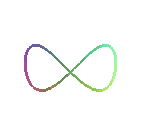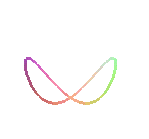
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
BESACE
Besace,
Quersackkurve
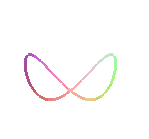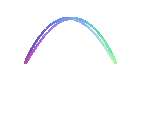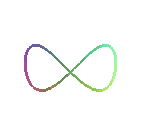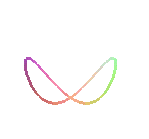
| Courbe étudiée et ainsi nommée par Cramer en 1750. |
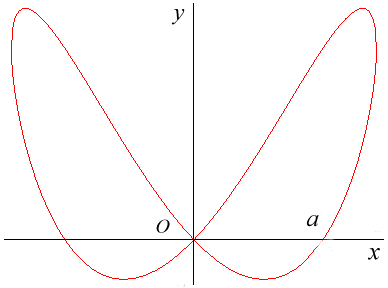 |
Équation cartésienne :
ou encore
ou Quartique
rationnelle.
|
Étant donné un diamètre [AB] et un point O d'un cercle (C), la besace associée est le lieu des points M d'une droite variable (D) parallèle à (OA) tels que QM = OP où P est un point d'intersection de (D) et (C) et Q le projeté de O sur (D), (ici, A(a, 0) et B(0, b)).
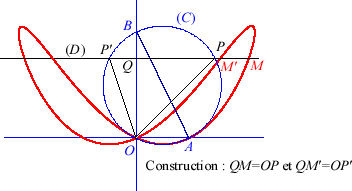
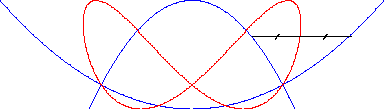
La troisième forme de l'équation cartésienne
montre que les besaces sont les courbes polyzomales
médianes entre les paraboles coaxiales
et
.
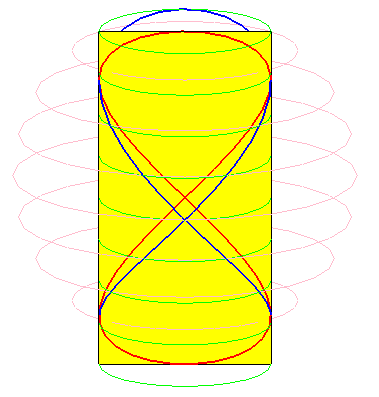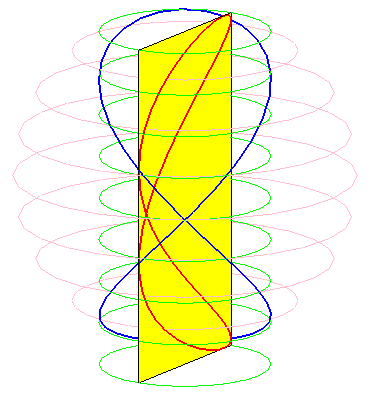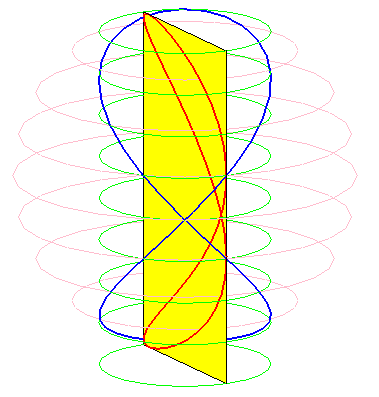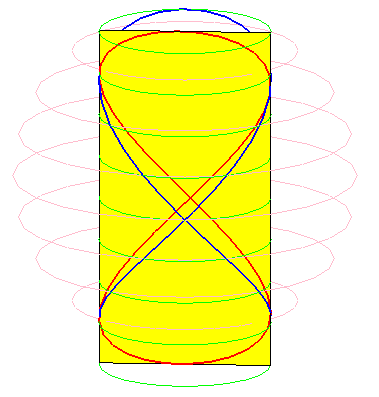
Les besaces sont les projections de la fenêtre de Viviani sur les plans passant par l’axe du cylindre sur lequel cette fenêtre est découpée.
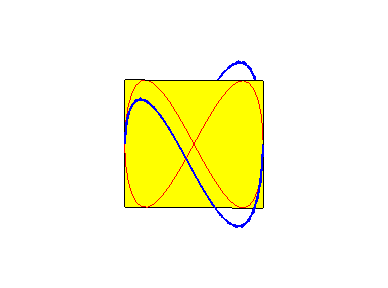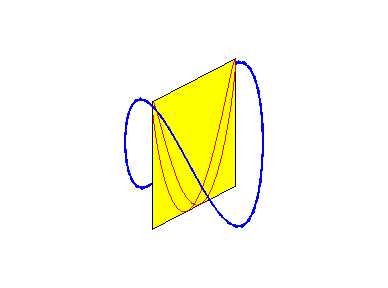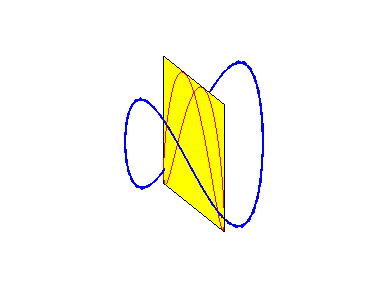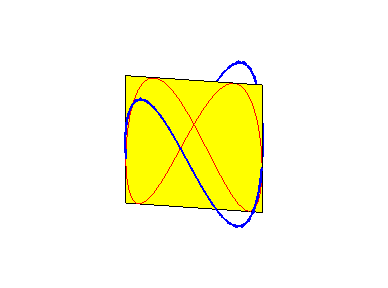
Lorsque b = 0 (i.e. lorsque le cercle est tangent
à Oy), on obtient la lemniscate
de Gerono et lorsque a = 0, un arc de parabole.
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL
2000