COURBE DE LISSAJOUS
Bowditch
curve (or Lissajous curve), Lissajoussche Kurve
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
COURBE DE LISSAJOUS
Bowditch
curve (or Lissajous curve), Lissajoussche Kurve
Ceux qui voient ce mouvement dans la figure rouge sont, parait-il, "cerveau droit", ceux qui voient le mouvement inverse seraient "cerveau gauche".... |
Pourquoi n'arrive t-on pas à voir ce mouvement dans la figure rouge ? |
| Courbe étudiée par Bowditch
en 1815 et par Lissajous
en 1857.
Autres nom : figure de Lissajous, courbe de Bowditch. Pour les intimes : joue courbe d'Alice (contrepéterie dûe à André Délédicq). Nathaniel Bowditch (1773-1838) : navigateur et mathématicien américain. Jules Lissajous (1822-1880) : physicien français. |
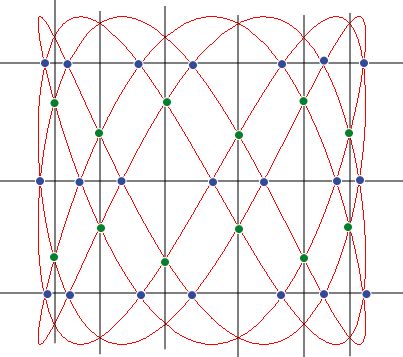
Paramétrisation cartésienne réduite: 
(  ). |
Les courbes de Lissajous sont les trajectoires d'un point dont les composantes rectangulaires ont un mouvement sinusoïdal.
Les courbes de Lissajous de paramètre n
(rapport des pulsations des deux mouvements sinusoïdaux) sont les
projections sur les plans passant par l'axe des couronnes
sinusoïdales de paramètre n :
ainsi que des couronnes sinusoïdales de paramètre
1/n : 
.
La courbe de paramétrisation réduite de
l'en tête est en effet projection sur xOy de la couronne
sinusoïdale d'axe Oy et de paramètre n : 
et projection sur xOy de la couronne sinusoïdale d'axe Ox
et de paramètre 1/ n :
.
Si n est irrationnel, la courbe est dense dans
le rectangle 
.
Si n est un rationnel de forme irréductible 
,
il est plus agréable de prendre les équations suivantes :
Paramétrisation cartésienne : 
, 
.
Courbe algébrique de degré 2q si 
pour p impair ou 
pour p pair.
Portion de courbe algébrique de degré q si 
pour p impair ou 
pour p pair.
Le nombre de points doubles vaut, en général, 
( p–1 groupes de q points alignés sur des droites
parallèles à Ox, en bleu ci-contre, et q–1
groupes de p points alignés sur des droites parallèles
à Oy, en vert ci-contre).
Dans le cas où la courbe est à double sens de parcours, il y a 
points doubles. |
 |
On obtient une portion de la courbe du n-ième
polynôme de Tchebychef Tn
pour n entier pair,
et pour n entier impair, 
.
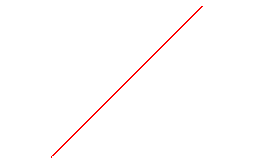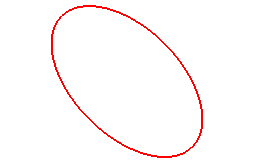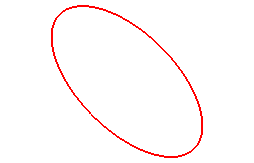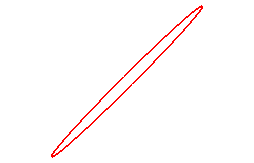
Voici quelques cas particuliers, avec a = b :
Pour n = 1, on obtient les ellipses :
 |
 |
 |
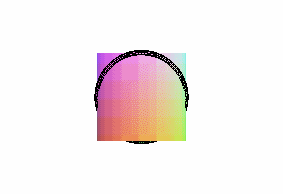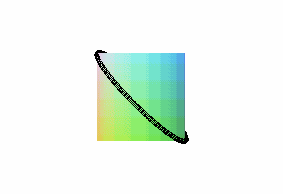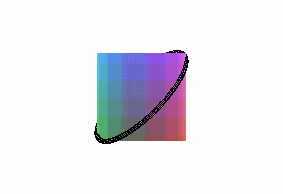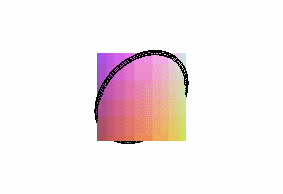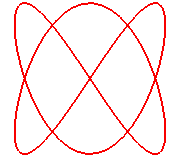
Pour n = 2 (q = 2, p = 1), on obtient
les besaces :
 |
 |
: lemniscate de Gerono |
 : portion de
parabole. |
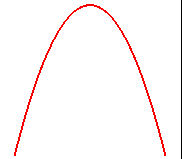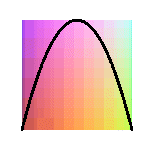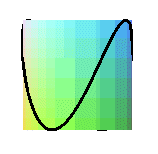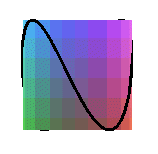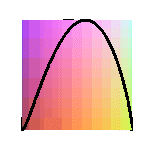
projections de la couronne sinusoïdale de paramètre 2 ( courbe de la crêpe) |
 |
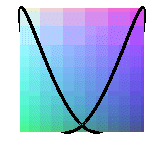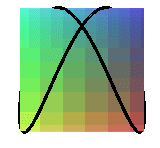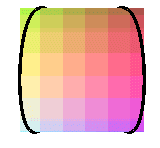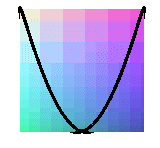
projections de la couronne sinusoïdale de paramètre 1/2 ( fenêtre de Viviani) |
Pour n = 3/2 (q = 3, p = 2) :
 |
 |
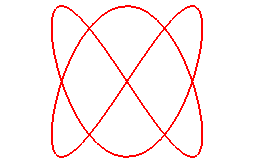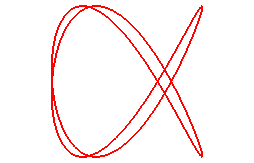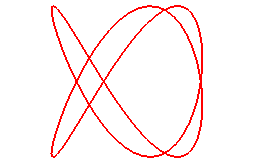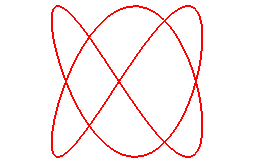:  Sextique d'équation cartésienne |
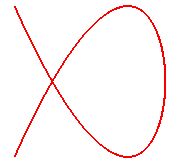  Portion de la parabole
divergente d'équation cartésienne: |
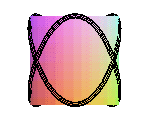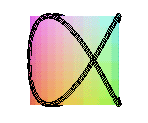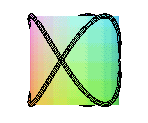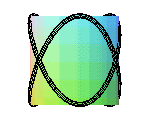
couronne sinusoïdale de paramètre 3/2 |
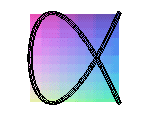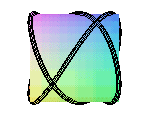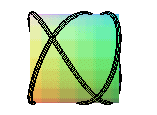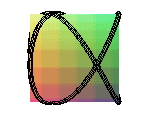
couronne sinusoïdale de paramètre 2/3 |
Pour n = 4/3, (q = 4, p = 3) :
 |
 |
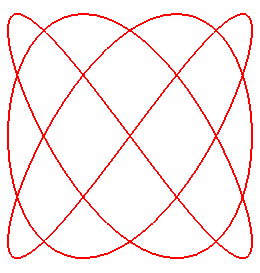Paramétrisation cartésienne (courbe
de droite):
ou 
( )
Équation cartésienne : En voir ici
une version nouée.
|
n = 5/3
 |
n = 5/4
 |
n = 6/5
 |
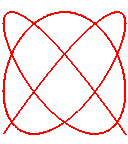n = 8/5
 |
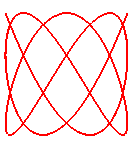n = 9/8
 |
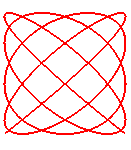| Les courbes de Lissajous ont la même topologie
que les courbes de boules dans un billard rectangulaire.
Voir cette page. |
 |
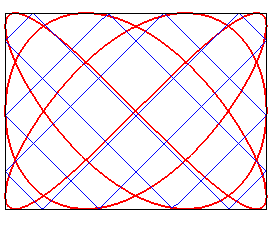On peut aussi imaginer des "courbes de Lissajous en coordonnées
polaires", de paramétrisation polaire : 
; ci-contre le cas p = 3, q = 7, 
(idée de Ch. de Rivière). |
 |
| Ce beau paillasson, ou "paillet", ou encore "baderne",
ne suit pas exactement une courbe de Lissajous.
Cependant, si dans la courbe de Lissajous |
 |
 |
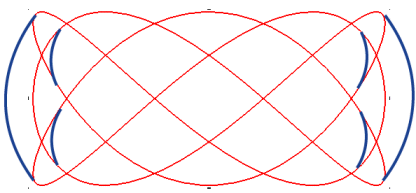Voir aussi les courbes
de Lissajous 3D, et les vasques.
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL, Jacques MANDONNET 2015
.
,
vous suivez les "ponts" bleus ci-contre, vous obtenez le paillasson.