| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
| Courbe étudiée par Ménechme
au 4ème siècle avant J.C., puis par Archimède, Apollonius,
Pappus, Galilée etc...
Du grec parabolê "comparaison, parabole", de para "à côté de", et ballein "lancer". |
 Longueur de l'arc de parabole :
|
Équation cartésienne réduite : Conique polynomiale. p (> 0) : paramètre de la parabole. F(p/2, 0) : foyer de la parabole. (D), droite d'équation x = – p/2 : directrice de la parabole. Paramétrisation cartésienne réduite : Équation polaire : Abscisse curviligne : Rayon de courbure : Équation polaire (pôle F, axe Fx) : |
La parabole est la conique d'excentricité 1.
Elles a été historiquement définie comme section de cône de révolution par un plan parallèle à une génératrice :

La parabole possède de nombreuses définition géométriques planes :
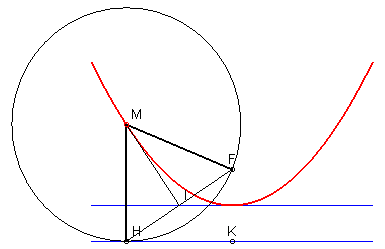
1) Définition par foyer et directrice :
La parabole est la courbe
d'équidistance entre un point (le foyer F) et
une droite (la directrice (D)) , autrement dit une isotèle
de droite, d'où la construction :
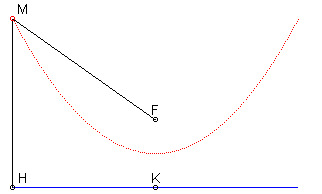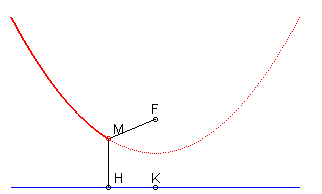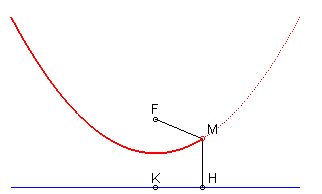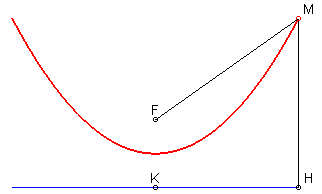
MF = MH
|
La parabole est la courbe d'indécision fatale de l'âne de Buridan deavant choisir entre une carotte et de l'eau ! |
| Le lieu des points M dont la somme des distances
à un point F et à une droite D est constante
égale à d est donc la réunion de deux arcs
de paraboles de foyer F et de directrices situées à
distance d de D.
D'où la construction d'un arc de parabole par une méthode similaire au tracé du jardinier pour les ellipses. |
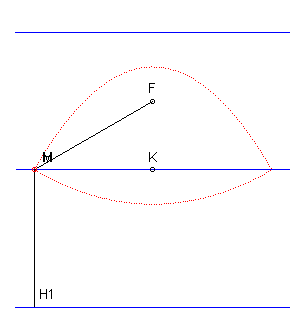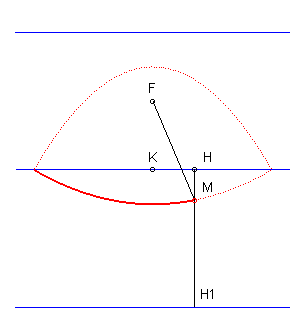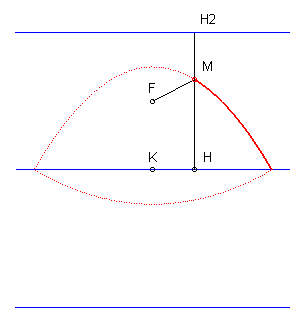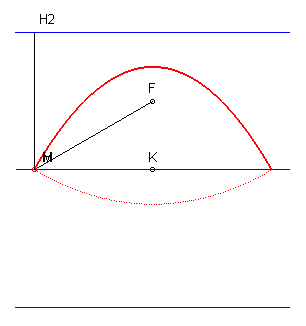 |
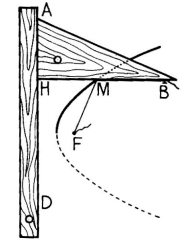
Figure tirée de la bible : le Lebossé Hémery |
| Plus généralement les courbes d'équidistance entre un cercle et une droite sont des réunions de deux paraboles : |
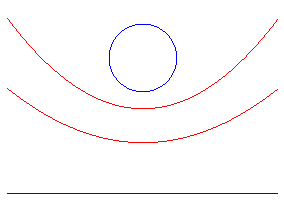
voir ici le tas de sable correspondant. |
La construction des foyer et directrice de la parabole
définie comme section d'un cône est donnée par le théorème
de Dandelin illustré ci-dessous :
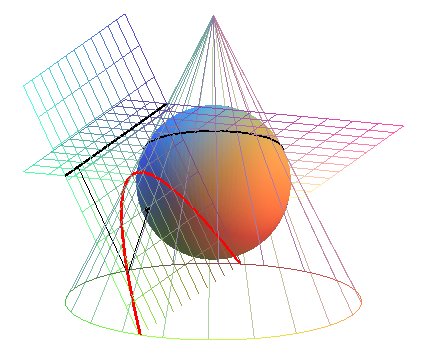 |
La sphère inscrite dans le cône et tangente au plan de la parabole l'est au foyer de la parabole, et le plan du cercle de contact coupe le plan de la parabole en la directrice. |
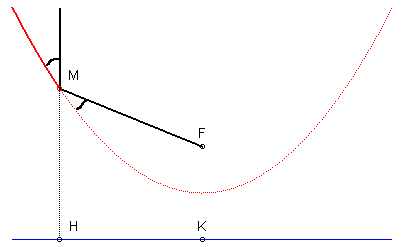
De plus, la tangente en M est la bissectrice intérieure de l'angle FMH :
Applications :
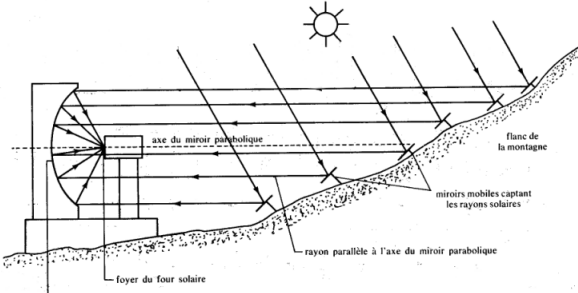
|

Pour envoyer la balle dans le trou, l'envoyer parallèlement au bord ! |
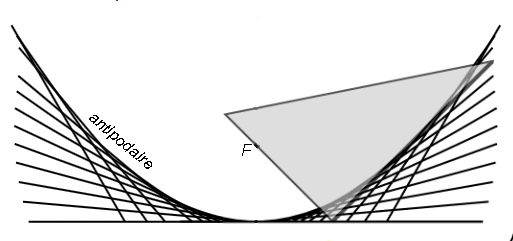
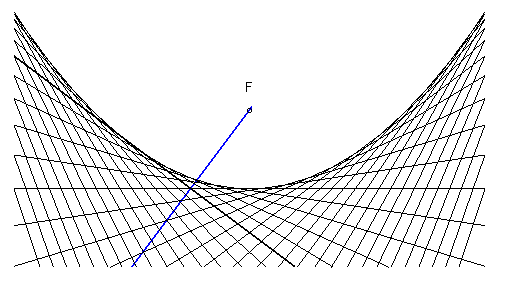
2) Définition par antipodaire de droite.
La parabole est l’enveloppe de la perpendiculaire en
I
à
la droite (FI), I décrivant la tangente au sommet
de la parabole (x = 0) (autrement dit, la parabole est l’antipodaire
de cette droite par rapport au foyer) ; c'est donc aussi l’enveloppe de
la médiatrice du segment [FH], H décrivant
la directrice (autrement dit, l’orthotomique
de la parabole par rapport à son foyer est la directrice).
 |
Application 1 : métode de construction avec une équerre. |
 |
3) La parabole est l’enveloppe d’une droite passant par
deux points ayant des mouvements rectilignes uniformes (voir aussi à
courbe
de Lamé).
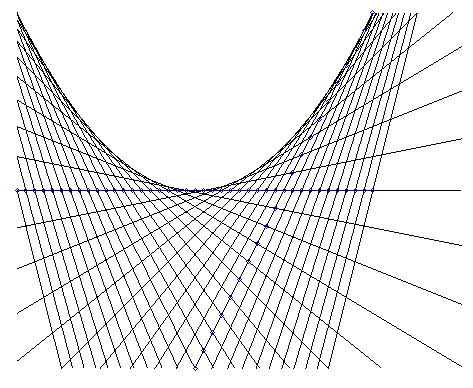 |
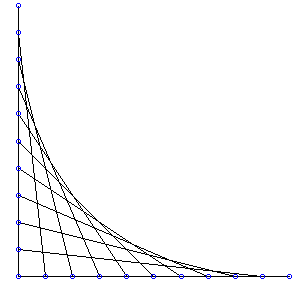 Les courbes que l’on obtient dans les tableaux de fils à montants rectilignes sont donc des arcs de parabole, et non des arcs de cercles comme on pourrait le penser hâtivement. |
4) La parabole est une anticaustique de droite.
5) La parabole est une courbe de Ribaucour.
6) La parabole est la courbe à sous-normale
constante ()
ou la courbe à sous-tangente
double de l’abscisse (
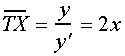
Les podaires de parabole sont les cubiques circulaires rationnelles (voir à podaire).
La développée
de la parabole
est la parabole
semi-cubique ;
.
Remarquons que les paraboles sont toutes semblables entre elles, et que l'image d'une parabole par n'importe quelle transformation affine est une parabole, donc semblable à la parabole de départ.
Les trajectoires d'un point matériel dans un champ
de pesanteur constant sont des droites ou des paraboles :
|
|
 |
et de même, les courbes d'écoulement d'un plan incliné sont des droites ou des paraboles.
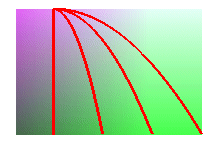
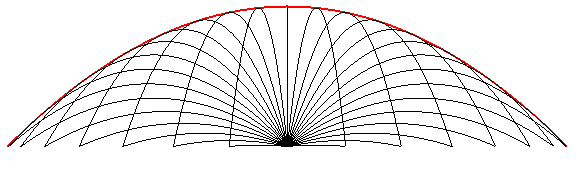 |
L'enveloppe de toutes les trajectoires des tirs issus
d'un point donné avec une vitesse de départ constante est
aussi une parabole dénommée parabole de tir ou de sûreté.
Voir à courbe balistique ce que tout ceci devient avec un frottement fluide. |
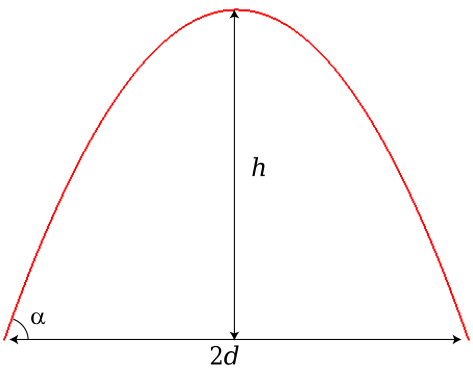
Equation d'un tir parabolique : Équation de la parabole de sûreté : avec Comme il se doit, le point de tir est au foyer de la parabole de sûreté. Distance de tir : Hauteur du tir : Longueur du tir : |
| On obtient également une parabole en faisant tourner
à vitesse constante un liquide coincé entre deux plaques
de verre ; le paramètre de la parabole est égal à |

exemple avec g = 10 et omega = 5 radians par seconde |
| La courbe théorique du câble supérieur d'un pont suspendu est assimilable à une parabole, mais pas celle d'un fil pesant suspendu libre, qui prend la forme d'une chaînette. |  |
| Idem pour l'arche d'un viaduc comme celui de Garabit : |
 |
Voir les parallèles à la parabole ici.
Voir aussi la courbe
du nageur et les paraboloïdes.
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2009