CHAÎNETTE
Catenary
or funicular curve, Kettenlinie
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
CHAÎNETTE
Catenary
or funicular curve, Kettenlinie
| Courbe étudiée par Leibniz, Jean Bernoulli
et Huygens en 1691.
Sous sa forme latine catenaria, le nom est dû à Huygens. Autres noms : courbe funiculaire, vélaire. On trouve la dénomination de caténoïde (féminin) pour les courbes affines de la chaînette. Il faut alors bien dire "le" caténoïde pour parler de la surface. Voir aussi : www.mathouriste.eu/Catenaire/Catenaire_Chainette.html |
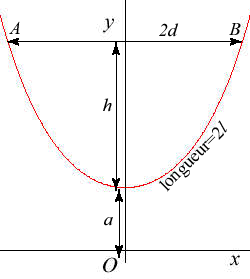 La relation entre la longueur 2l, la flèche
h
et la largeur 2d
|
Équation différentielle :  .
Équation cartésienne : 
.
L'axe des x en est la base, celui des y, l’axe de symétrie. Paramétrisation cartésienne : 
,
ou 
, avec  .
Abscisse curviligne : 
.
Rayon de courbure : 
(égal à la normale
:  -> courbe
de Ribaucour).
Équation intrinsèque 1 : 
(cas particulier d'alysoïde).
Équation intrinsèque 2 : 
(voir les notations).
Courbe transcendante. |
La chaînette est la forme prise par un fil pesant
flexible infiniment mince homogène inextensible suspendu entre deux
points, placé dans un champ de pesanteur uniforme. Galilée
a posé le problème et constaté que la courbe suivie
par le fil était approximativement un arc de parabole,
l'approximation s'améliorant quand on étend le fil. Ce sont
Leibniz, Jean Bernoulli, et Huygens qui ont trouvé, indépendamment
en 1691, les bonnes équations.
Avec les notations de la figure ci-contre (
= tension du fil en M,  =
masse linéique du fil) , écrivons que la somme des forces
en M est nulle : 
Ceci se simplifie en |
 |
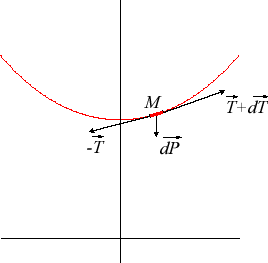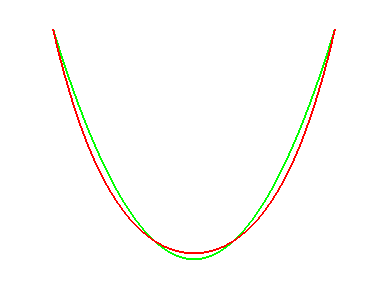
Apprenons à différencier les chaînettes
des paraboles :
 
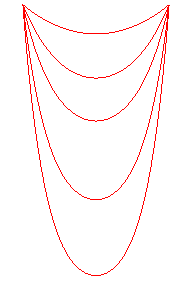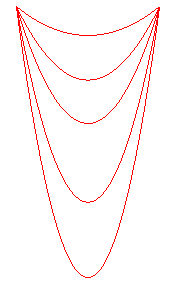
pour une même longueur, les paraboles sont plus "pointues" |
 |
Voir la courbe
du pont suspendu, ainsi que la chaînette
élastique, qui joignent la parabole à la chaînette.
Comme pour le fil suspendu, une voûte formée
de pierres jointives tenant par leur propre poids prend aussi une forme
de chaînette, renversée (propriété dite de la
voûte de Poinsot- (démonstration
:
Brocard part. comp. p 189))
:
 |
 |
La "Gateway Arch" à St Louis dans le Missouri est en forme de chaînette. |
Terrasse de la casa mila, de l'architecte Gaudi à Barcelone. |
Chaînette de conteneurs au Havre. L'artiste Vincent Ganivet la dénomme : "catène". |
Hangar à dirigeables d'Ecausseville |
Pour les surfaces de révolution ayant la même
propriété, voir à dôme
de Bouguer.
Par contre, les arches des ponts ont, elles, un profil
parabolique (pont suspendu à l'envers...)
Le viaduc de Garabit a une arche parabolique (et non circulaire comme
le disent les cartes postales)
La chaînette est aussi le profil d’une voile rectangulaire attachée à 2 barres horizontale, enflée par un vent soufflant perpendiculairement à ces barres, en négligeant le poids propre de la voile par rapport à la force du vent, d'où le nom de "vélaire" donné par Jacques Bernoulli.
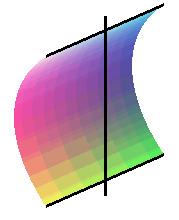
L'arc de courbe joignant deux points donnés A et B dont la rotation autour d'une droite (D) coplanaire avec (AB) engendre une surface d'aire minimale est l'arc de chaînette de base (D) passant par A et B ( voir à caténoïde).
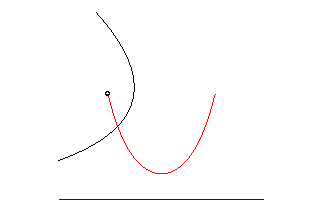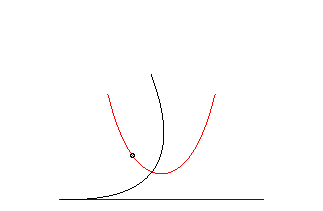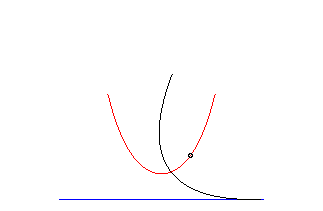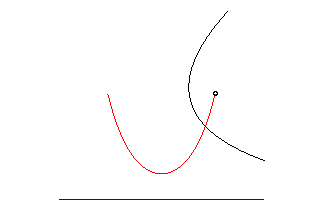
La chaînette est quand même liée à la parabole par le fait que 'elle est aussi une roulette parabolique de Delaunay : lieu du foyer d'une parabole roulant sans glisser sur une droite.
La chaînette est la seule courbe dont le rayon de courbure est égal à la normale ; l'unique surface de révolution à courbure moyenne nulle a donc pour méridienne la chaînette : c'est le caténoïde ; on en déduit aussi que la chaînette est un cas particulier de courbe de Ribaucour.
La chaînette est aussi la caustique par réflexion de la courbe exponentielle y = a ex/a pour des rayons parallèles à Oy.
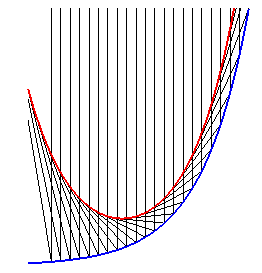
La développée
de la chaînette est la courbe de paramétrisation :  . |
 |
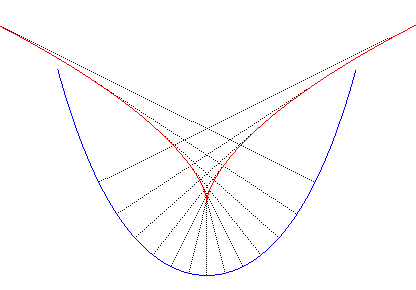| La développante principale de la chaînette
est la tractrice dont l'asymptote
est la base de la chaînette.
On en déduit qu’un point fixe dans le plan lié à une droite roulant sans glisser sur la chaînette, coïncidant avec le centre O de la chaînette quand la droite est tangente à son sommet, décrit la droite Ox. |
 |
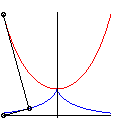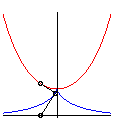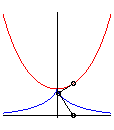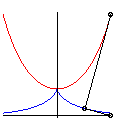Ce phénomène permet de faire rouler des roues polygonales sur des arcs de chaînette de façon à ce que le centre de la roue se déplace en ligne droite.
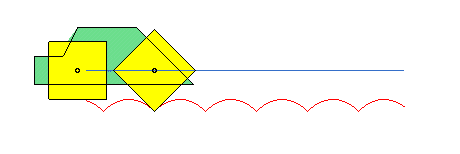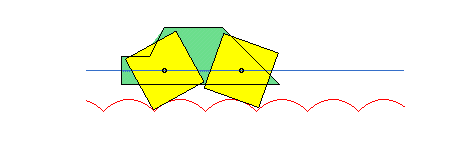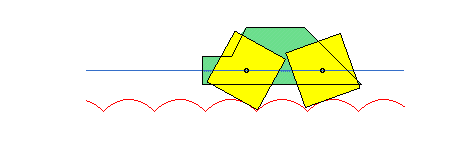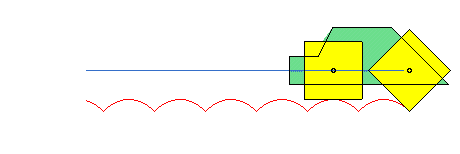
Si on enroule le plan de la chaînette en un cylindre de révolution d'axe vertical, celle-ci devient une pseudo-géodésique de ce cylindre.
Voir aussi l'alysoïde, la chaînette élastique, la courbe du pont suspendu, la chaînette d'égale résistance, la chaînette électro-dynamique, la courbe de la corde à sauter, et la lintéaire.
La notion de chaînette se généralise
à un fil placé
sur une surface, avec comme cas particulier la chaînette
sphérique.
 |
Les fils du téléphériques forment une chaînette quand ils sont libres, mais le haut du téléphérique, lui, décrit un arc elliptique.... |
 |
 |
Sont-ce des chaînettes ?
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL, Jacques MANDONNET 2014
,
d'où en éliminant 
, la relation : 
soit 
.
,
qui par intégration donne 
.
qui
est bien l'équation différentielle intrinsèque 2 donnée
ci dessus (voir les