Le terme caustique désigne d’une façon générale l’enveloppe des rayons lumineux issus d'un point à distance finie (caustique "au flambeau") ou infinie (caustique "au soleil ") après modification par un instrument optique. On considère le rayon modifié en entier, y compris la demi-droite virtuelle.

A) CAUSTIQUE PAR REFLEXION

Dans le plan, la caustique par réflexion (ou catacaustique) d'une courbe  pour une source lumineuse S est l'enveloppe des rayons issus de S après réflexion par  considérée comme le profil d'un miroir.

    I) Cas où S est à distance finie.
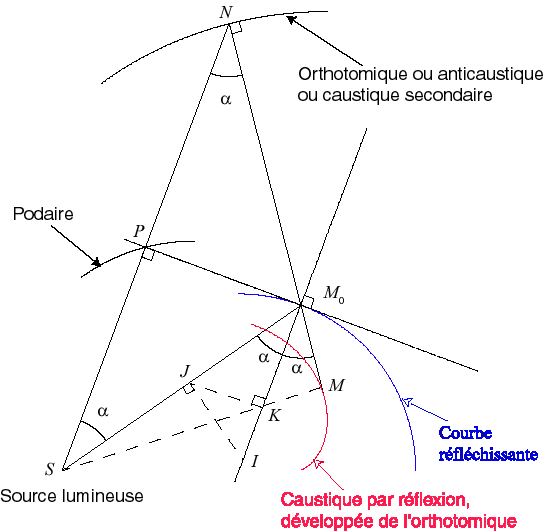
Dans ce cas, la caustique par réflexion de la courbe réfléchissante  est la développée de la courbe orthotomique, appelée dans ce cas plutôt anticaustique, ou caustique secondaire ; rappelons que cette courbe est elle-même image de la podaire de  par rapport à S dans une homothétie de centre S et de rapport 2.
 
 

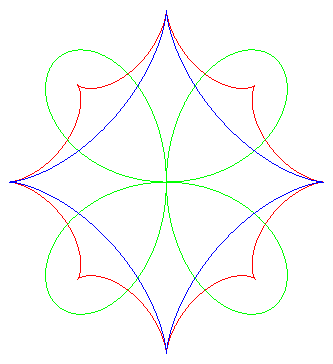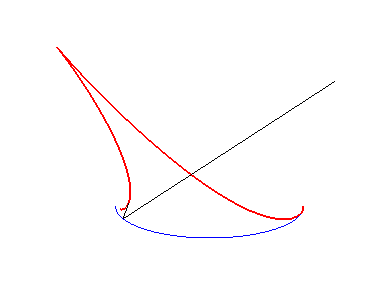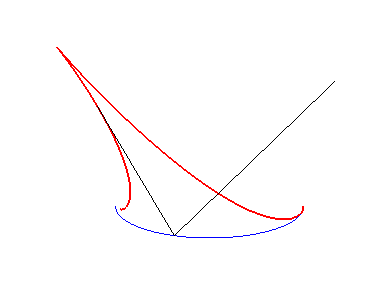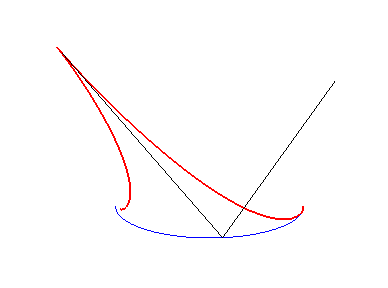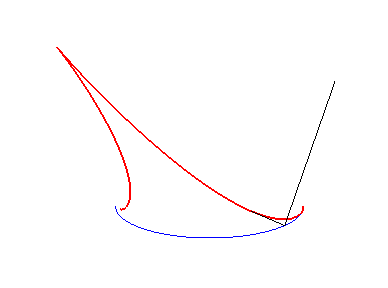
Construction du point caractéristique M du rayon réfléchi : on projette le centre de courbure I en M0 en J sur le rayon incident, puis en K sur la normale en M0 : S, K et M sont alignés.	La caustique rouge est la développée de l'orthotomique verte de l'ellipse bleue.	La caustique rouge est la développée de l'orthotomique verte de l'astroïde bleue.

Application de ce résultat : l’antipodaire d’une courbe cycloïdale a pour caustique par réflexion une courbe cycloïdale semblable.

Exemples :
 

courbe réfléchissante (ou dirimante)	source lumineuse	caustique par réflexion
cercle	sur le cercle et au sommet de la cardioïde	cardioïde
cercle	quelconque pôle du limaçon	caustique de cercle
parabole	foyer de la parabole	se réduit au point à l'infini dans la direction de la parabole
conique bifocale	foyer de la conique	se réduit à l’autre foyer
spirale logarithmique	point asymptote de la spirale	spirale logarithmique
cubique de Tschirnhausen	foyer	parabole semi-cubique
cissoïde de Dioclès	point (4a, 0)	cardioïde
cardioïde	point de rebroussement	néphroïde
caustique inverse de cercle	centre	cercle

    II) Cas où S est à l'infini.

Dans ce cas (les rayons incidents sont parallèles), la caustique peut aussi se construire comme développée ; une droite D orthogonale aux rayons étant choisie, la caustique est la développée de l'anticaustique associée à la droite D , lieu du symétrique par rapport à la tangente en M₀ du projeté de M₀ sur D ; remarquons que les différentes anticaustiques associées aux droites D sont parallèles et ont donc la même développée.

Construction de la caustique au soleil à partir d'une anticaustique ; le point caractéristique du rayon réfléchi en M₀ se détermine comme projeté sur ce rayon du milieu du segment joignant M₀ au centre de courbure de (G₀) en M₀ :

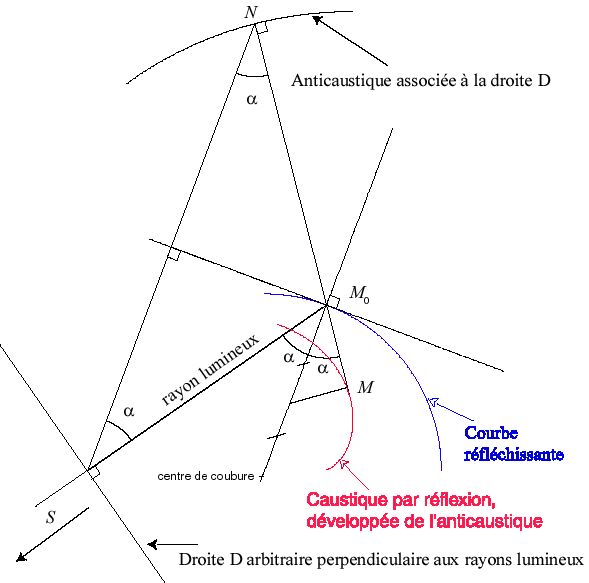
Paramétrisation cartésienne pour des rayons parallèles à Ox :

Exemples :
 

courbe réfléchissante ou caustique inverse	direction des rayons	caustique
cercle	quelconque	néphroïde (courbe de la tasse de café)
parabole	parallèle à l'axe	foyer
parabole	toute autre direction	cubique de Tschirnhausen
parabole cubique ay2=x3	parallèle à Oy	cubique de Tschirnhausen
parabole généralisée  (; le cas k=1/2 est le cas précédent)	parallèle à Oy	courbe de poursuite (k =vitesse du maître / vitesse du chien)
logarithmique : y = a ln (x/a)	parallèle à Oy	courbe de poursuite (vitesse du maître = vitesse du chien)
arche de cycloïde	perpendiculaire à l'axe de roulement	deux arches de cycloïde réduites de moitié
deltoïde	quelconque	astroïde
courbe exponentielle y = a ex/a	parallèle à Oy	chaînette

B) CAUSTIQUE PAR RÉFRACTION (généralisant le cas précédent)

La caustique par réfraction (ou diacaustique) d'une courbe  pour une source lumineuse S est l'enveloppe des rayons issus de S après réfraction par  considérée comme le profil d'un dioptre.

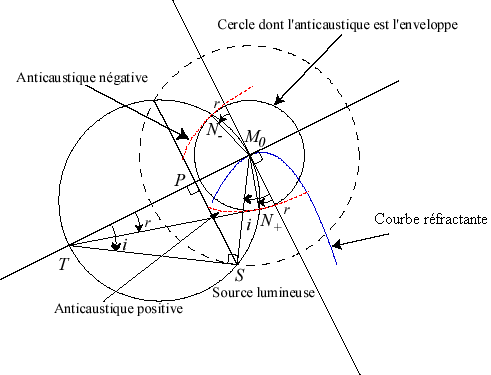
Si M₀ est un point de la courbe  et n une constante (qui peut être négative), le rayon réfracté du rayon incident (SM₀) est la droite (D) faisant un angle r avec la normale (N) à  en M₀, avec , où i est l'angle .

Seul le cas n > 0 correspond à la réfraction physique (n est alors le rapport  des indices de réfraction de l'autre côté de S et du côté de S) ; le cas n = –1 redonne le cas de la réflexion.

On désigne par caustique par réfraction complète pour la constante n > 0 la réunion des caustiques pour les constantes n et –n ; c'est la développée de l'anticaustique de  par rapport à S associée à la constante n.

Exemples :
    - les caustiques par réfraction complètes de la droite sont les développées de coniques et les caustiques par réfraction complètes du cercle sont les développées d'ovales de Descartes complets.
    - les courbes dont la caustique par réfraction est réduite à un point sont les coniques pour des rayons incidents paralèles, et les ovales de Descartes pour des rayons provenant d'un source à distance finie.

Voir aussi sur cette page l'exemple des caustiques par réfraction des cercles, pour une source à l'infini.

C) ORTHOCAUSTIQUE.
L'orthocaustique de  pour la source S est l'enveloppe des perpendiculaires aux rayons issus de S au point d'impact sur . L’orthocaustique n’est donc autre que l’antipodaire.

Exemples : l'orthocaustique d'une droite (D) est la parabole de foyer S tangente à (D) ; l'orthocaustique d'un cercle (C) est l'ellipse ou l'hyperbole de foyer S bitangente à (C).

D) AUTRES CAUSTIQUES.
Pour un billard limité par une courbe convexe, on désigne aussi par "caustique" l'enveloppe des trajectoires successives d'une boule de billard (dans le cas où cette trajctoire est non périodique). Par exemple, pour un billard elliptique, la caustique est une ellipse ou une hyperbole homofocale (voir ce site).

Voir aussi, dans le domaine des courbes définies par des procédés optiques, les anamorphoses.
 
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL, Jacques MANDONNET 2016