Autre nom : anticaustique, mais ayant un autre sens dans ce site. Ref : (Zwikker p. 144)

 

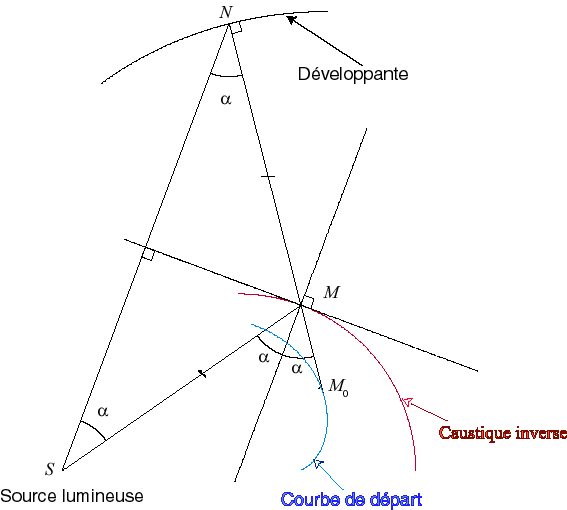
On désigne par caustique inverse (par réflexion) par rapport à un point S d'une courbe , toute courbe  dont la caustique par réflexion par rapport à S est . Si  est le point courant de  et M celui de , la condition est que la normale en M à la caustique inverse soit constamment bissectrice de . La caustique directe étant la développée de l'orthotomique, les caustiques inverses sont les courbes dont l'orthotomique est une des développantes de la courbe de départ. 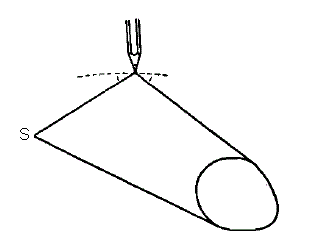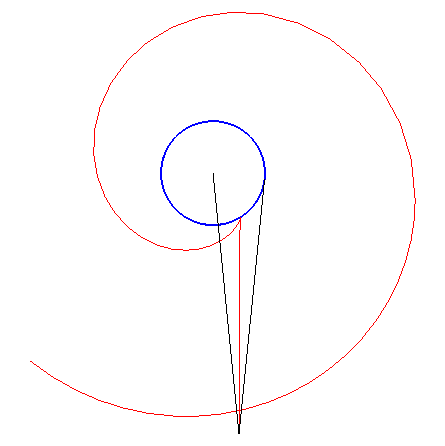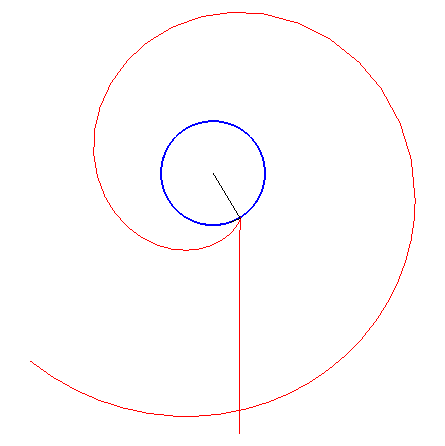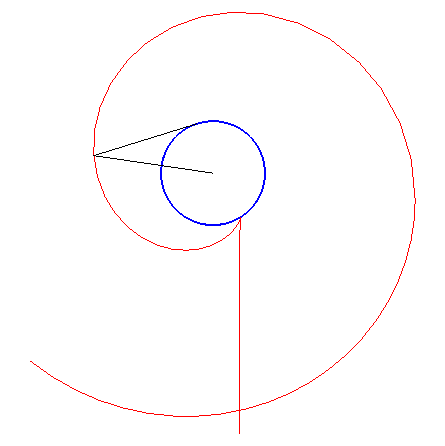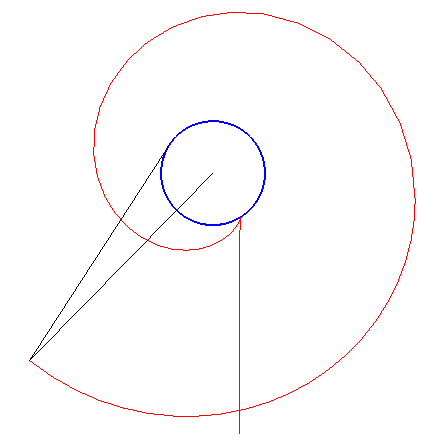Le schémas ci-contre montre la construction de M connaissant le point N de la développante.

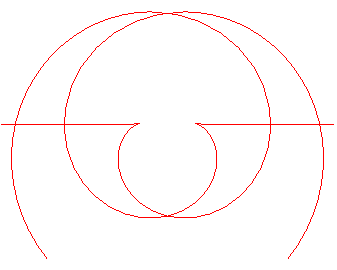
Lorque la courbe de départ est convexe, on obtient donc mécaniquement une portion de caustique inverse en enroulant un fil inextensible autour de cette courbe et en le faisant passer par S et par un crayon qui tracera la caustique inverse (généralisation de la méthode du jardinier pour le tracé des ellipses). Diverses longueurs de fil donneront diverses caustiques inverses.

 

Cas de la caustique inverse de cercle par rapport à son centre :
 
 

Paramétrisation cartésienne : , pour une caustique égale au cercle de centre O et de rayon 2a.

 
 
 

Les rayons lumineux issus du centre du cercle et réfléchis par la courbe rouge enveloppent le cercle bleu. On obtient la caustique inverse en déroulant sous tension une pelote de fil dont l'extrémité est accrochée au centre de la pelote.

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2012