Équation différentielle vectorielle : , se traduisant par le système différentiel :  , ou par le système : .

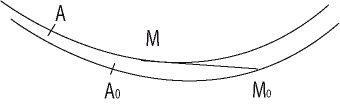
On appelle courbe de poursuite la trajectoire d'un mobile M (le chien ou l'avion chasseur) dont le mouvement est dirigé à chaque instant vers un autre mobile M0 (le lièvre ou le maître, ou l'avion chassé), dont la trajectoire est nommée courbe de fuite. On considère en général que les mouvements de M et M0 sont uniformes, de vitesses V et V0 = kV. La trajectoire de M0 étant donnée, celle de M est donc définie dans ce cas par le fait que (MM0 ) est tangente en M à sa trajectoire, et l'abscisse curviligne de M est proportionnelle à celle de M0 :.

Comme on pourrait s'y attendre, le chien rattrape le lièvre à coup sûr si et seulement s'il court plus vite que lui (k < 1) ; Lorsque les deux vitesses sont égales, la distance entre le chien et le lièvre tend au cours du temps vers une constante a, et la courbe du chien tend à devenir la tractoire de celle du lièvre avec une laisse de longueur a.

I) Cas le plus simple : la courbe de fuite est rectiligne.

Le lièvre décrit Oy à la vitesse V, et le chien le poursuit à la vitesse V/k.
 

Le chien ayant pour cordonnées (x, y), les données se traduisent par les relations :
ce qui fournit l’équation différentielle de la trajectoire du chien :	, soit  (car x décroit)
Si le chien est en A de coordonnées (a, b) quand le lièvre est en O, l'intégrale première est :	où  avec
et on obtient la courbe d'équation :	avec  si k ¹ 1 et  si k = 1
La loi horaire étant donnée par :	si  k ¹ 1   si k = 1.

La courbe est algébrique ssi k est rationnel : si k = p/q avec p et q premiers entre eux, le degré est 2p pour k > 1 et p + q pour k < 1.

En particulier, pour k = 1/2, on obtient une demi-cubique de Tschirnhausen (équation complète : ).

Le chien rattrape le lièvre ssi k < 1, et il le rattrape en (0, b – f(a)), soit  si b = 0.
Lorsque k = 1, la distance entre le chien et le lièvre tend vers une constante, égale à c/2.
 

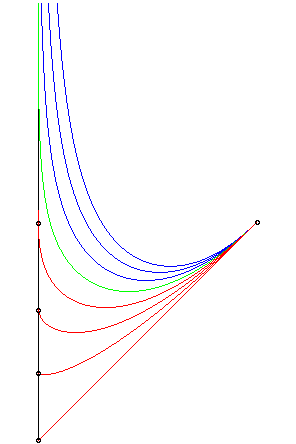
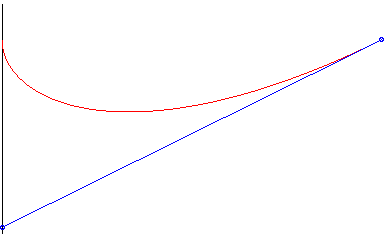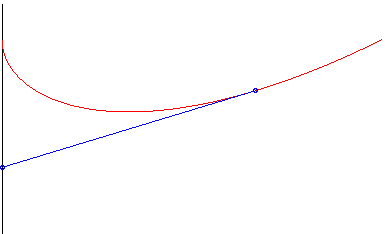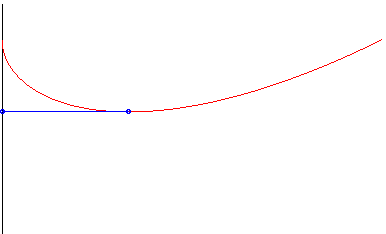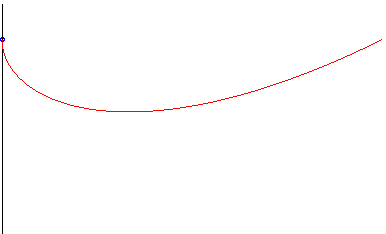
en rouge : le chien court plus vite que le lièvre : il le rattrape. en vert : il court aussi vite : pas de rattrapage possible, et en bleu, encore moins...

Le chien a même vitesse que le lièvre : leur distance tend vers une constante.

Remarquons que si le chien était intelligent et courait en ligne droite avec anticipation, il pourrait rattraper le lièvre ssi (pour b > 0) et pourrait donc toujours le rattraper s'il court aussi vite que lui.
 

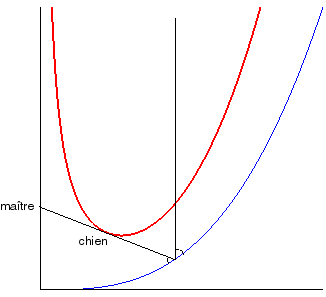
La courbe du chien pour  est la caustique par réflexion pour des rayons incidents verticaux de la parabole généralisée  avec  ; ci-contre, le cas k = 2 (parabole cubique). Dans le cas k = 1, la courbe du chien est la caustique par réflexion pour des rayons incidents verticaux d'une logarithmique.

Voir aussi les spirales anallagmatiques, qui sont les roues associées à ces courbes de poursuite.

II) Cas d'une courbe de fuite circulaire.
Pour le cercle de centre O et de rayon R, on obtient le système différentiel :  permettant de tracer les courbes à l'aide d'un logiciel.

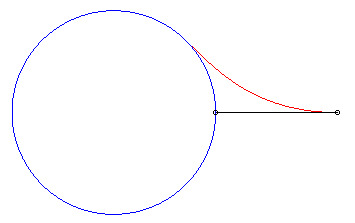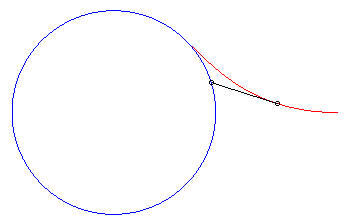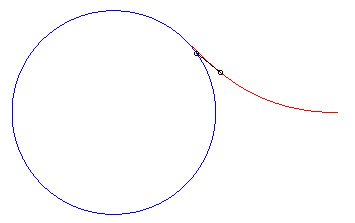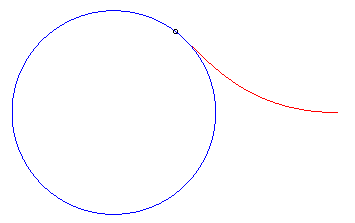
Le chien rattrape de nouveau son maître ssi k < 1 ; lorsque k = 1, la distance chien-maître tend vers 0, mais il ne le rattrape pas ; et lorsque k ³ 1, la courbe admet pour cercle asymptote le cercle de centre O et de rayon R/k, et la distance chien-maître tend vers .
 
 

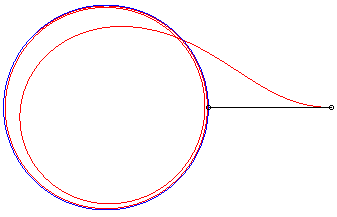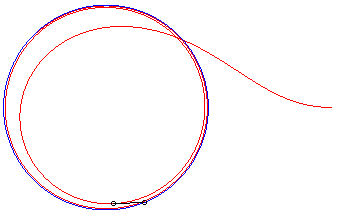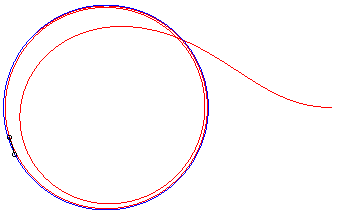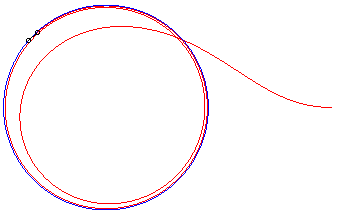Vchien = 2 Vmaître :  il le rattrape	Vchien = Vmaître :  il le rattrape... à l'infini.	Vchien = 1/2 Vmaître :  sa distance au maître tend vers  et il finit par tourner en rond sur un cercle de rayon R/2.

VARIANTE (sur une idée d'Alain Esculier) : la vitesse du chien n'est plus proportionnelle à celle du maître, mais à la distance à celui-ci.
 

Équation différentielle vectorielle : , se traduisant par le système différentiel : . Équations du mouvement du chien : .

I) Courbe de fuite rectiligne.
 

Pour un maître (vt, 0), équations du mouvement du chien passant par (0, b) : 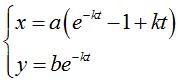 (a = v/k). Trajectoire du chien :. La vitesse du chien tend vers celle du maître, et leur distance mutuelle tend vers v/k.

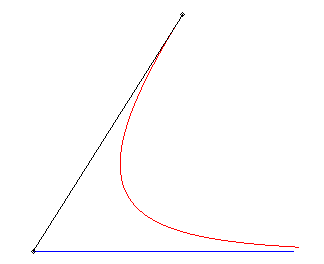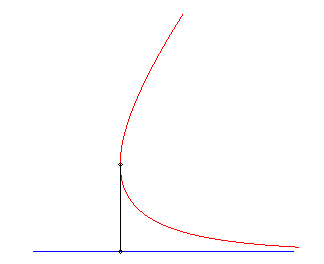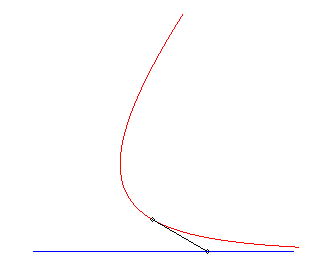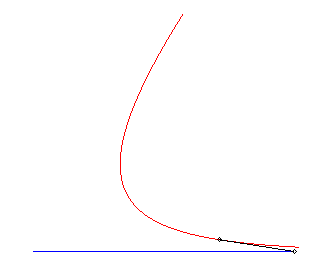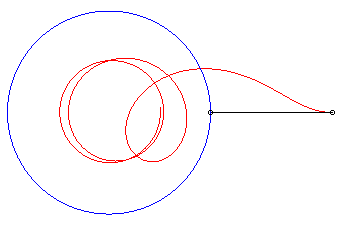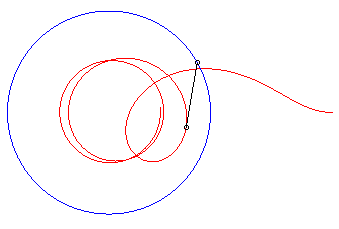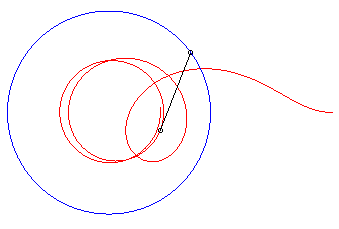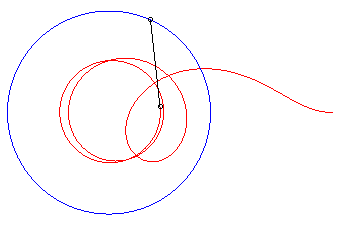
II) Courbe de fuite circulaire.
 

Pour un maître , équations du mouvement du chien passant par (0, 0) : . La  trajectoire du chien devient asymptote au cercle de centre O et de rayon , sa vitesse tend vers , et sa distance au maître tend vers .

Une généralisation consiste à considérer des courbes de poursuite où la vitesse du chien fait un angle constant avec la droite qui le joint au maître (en allemand, Schielwinkelkurve) ; le cas le plus simple est celui du maître immobile : le chien suit alors une spirale logarithmique.
Le cas d'un angle droit est étudié à courbe de Duporcq.

On peut aussi considérer des courbes de poursuite en 3D, et étudier des systèmes de poursuite.

Voir aussi les barycentriques.

Pour d'autres courbes suivies par des chiens, voir la courbe du nageur (chien nageant dans le courant vers son maître sur la berge) ou la conchoïde (chien tirant constamment sur sa laisse en direction d'un point fixe).
Comparer aussi avec la courbe de filature.
 
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2020