Équation différentielle vectorielle : .

On appelle courbe de poursuite la trajectoire d'un mobile M (le chasseur) dont le mouvement est dirigé à chaque instant vers un autre mobile M₀ (le chassé), dont la trajectoire est nommée courbe de fuite. On considère en général que les mouvements de M et M₀ sont uniformes, de vitesses V et V₀ = kV.

Comme on pourrait s'y attendre, le chasseur rattrape le chassé à coup sûr si et seulement s'il court plus vite que lui (k < 1) ; Lorsque les deux vitesses sont égales, la distance entre le chasseur et le chassé tend au cours du temps vers une constante a, et la courbe du chasseur tend à devenir la tractoire de celle du chassé avec une laisse de longueur a.

On peut aussi considérer des courbes de poursuites sur des surfaces : à tout instant, le chasseur se dirige sur la géodésique de la surface qui le joint au chassé.

Exemple : Courbe de poursuite sphérique ([Loria] p. 78).

Le chassé parcourt un grand cercle, et à tout instant, le chasseur se dirige sur le grand cercle qui le joint au chassé.
On montre que l'équation différentielle de la trajectoire en cordonnées sphériques (q = longitude, j = colatitude, le chassé parcourant l'équateur) est :

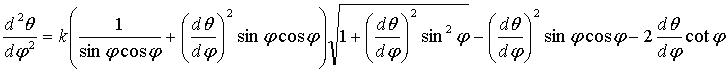
Voir les courbes de poursuite planes.

On peut aussi généraliser à l'espace les courbes de poursuites mutuelles ; en voici deux exemples :
 

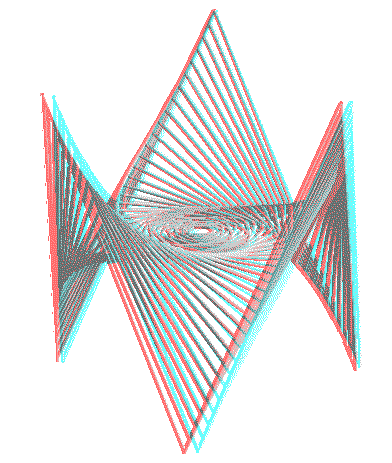
Réalisation Alain Esculier, anaglype à regarder avec des lunettes rouge (à gauche) et bleu (à droite)

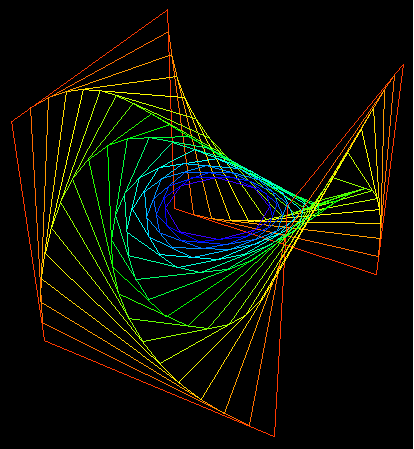
Envoyé par Emmanuel Amiot

 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2006