Vectorial differential equation: .

The notion of pursuit curve refers to the trajectory of a moving mass M (the hunter) the motion of which is constantly oriented towards another moving mass M₀ (the prey), the trajectory of which is called escape curve. In general, we consider that the motions of M and M₀ are uniform, with speeds V and V₀ = kV.

As can be expected, the hunter catches up with the prey with absolute certainty if and only if it runs faster than it (k < 1); when the two speeds are equal, the distance between the hunter and the prey goes to a constant a, and the curve of the hunter tends to become the tractory of that of the prey with a leash of length a.

We can also consider pursuit curves on surfaces: at every instant, the hunter moves along the geodesic of the surface that connects them to the prey.

Example: spherical pursuit curve ([Loria] p. 78).

The prey travels along a great circle, and at every instant, the hunter moves along the great circle that connects them to the prey.
It can be proved that the differential equation of the trajectory in spherical coordinates (q = longitude, j = colatitude, when the prey travels on the equator) is:

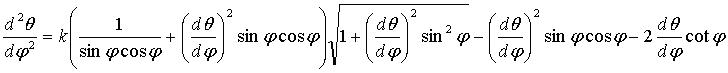
See the planar pursuit curves.

We can also generalize to space the mutual pursuit curves ; here are two examples.
 

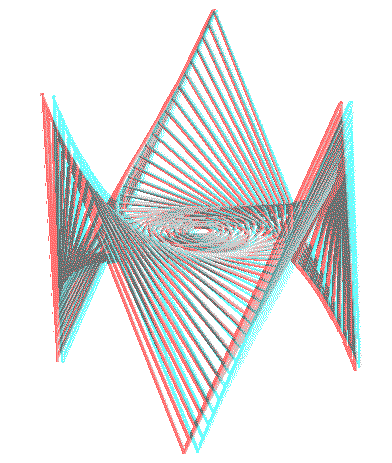
Made by Alain Esculier, anaglyph 3D to be looked at with red glasses (on the left) and blue (on the right)

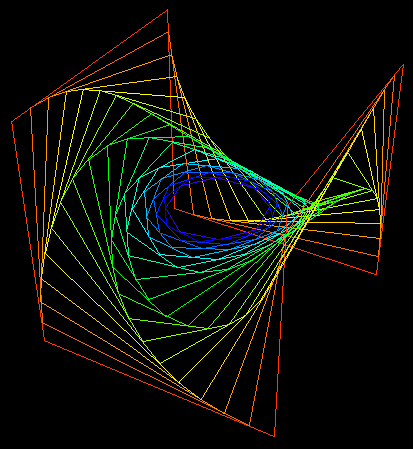
Sent by Emmanuel Amiot

 

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL  2018