TRACTORY
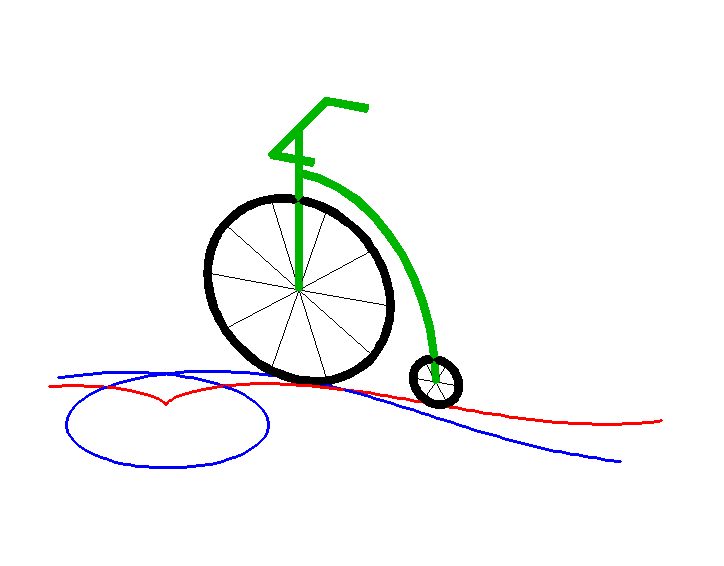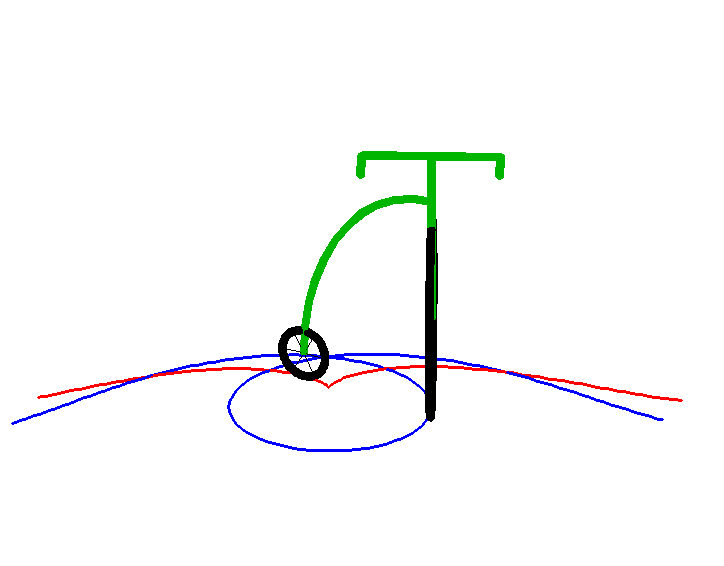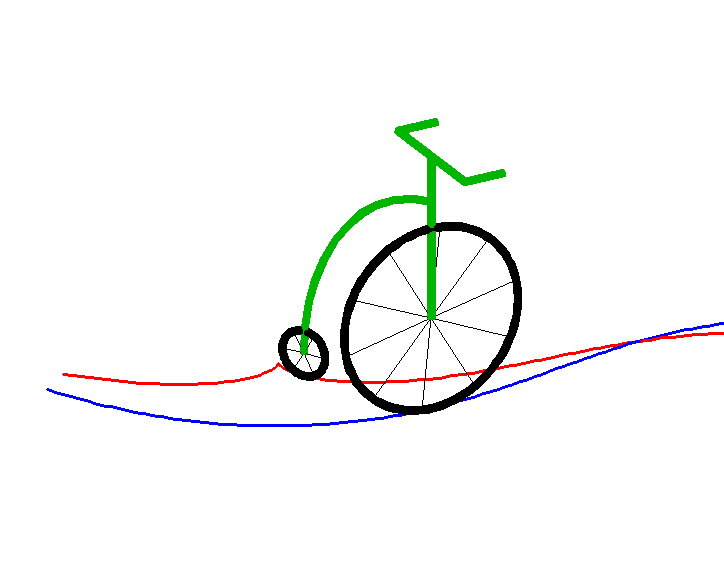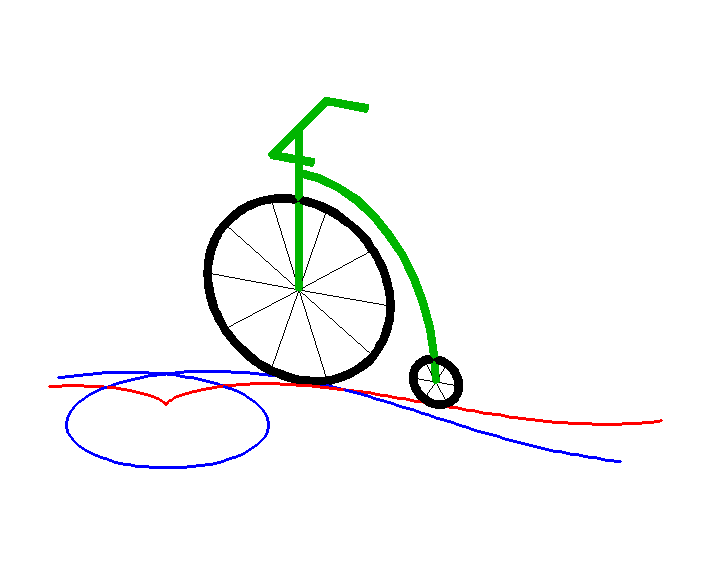
Animation by Alain Esculier
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
TRACTORY

Animation by Alain Esculier
| Other names: tractrix (but we chose to preserve this
name for the case where the base is linear), (recalcitrant) donkey curve.
Website: The traces of a bike Thérèse Eveilleau's bike |
| Differential equation: Cartesian parametrization: 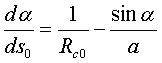 . . |
A curve (C) travelled along by a point M is a tractory
of a curve (C0) - the base - travelled
along by a point M0 if the length
of the segment line [M0M]
- the leash - remains constant and the line (M0M)
remains tangent to (C). For example, the back wheels of a car (or better,
of a bike) describe a tractory of the curve described by the front wheels
(forward or reverse gear).
Conversely, the curve (C0)
can be derived from the curve (C) by copying a constant length on the tangent
to (C); (C0) is then called equitangential
curve of (C).
As opposed to the notion of pursuit curve, this notion is not kinematic (the tractory does not depend on the speed of the point M); however, in a steady state, the pursuit curve of a dog running after a hare at the same speed is a tractory of the hare's trajectory.
Property: the normal at M0 to (C0) and the normal at M to the tractory (C) intersect at the centre of curvature of the tractory (hence the construction of the evolute of the tractory).
Remark: the equitangential curve can be seen as the glissette of a point on a line sliding on the curve.
Examples:
- the tractory of a line, which is the tractrix
- the tractory of a circle
- the tractory of the curve of constant gyration (defined by the fact that the leash forms with the tangent an angle proportional to the curvilinear abscissa).
Below, an animated view of an equitangential line (in blue) of a nephroid (in red); the nephroid is therefore a tractory of this curve.
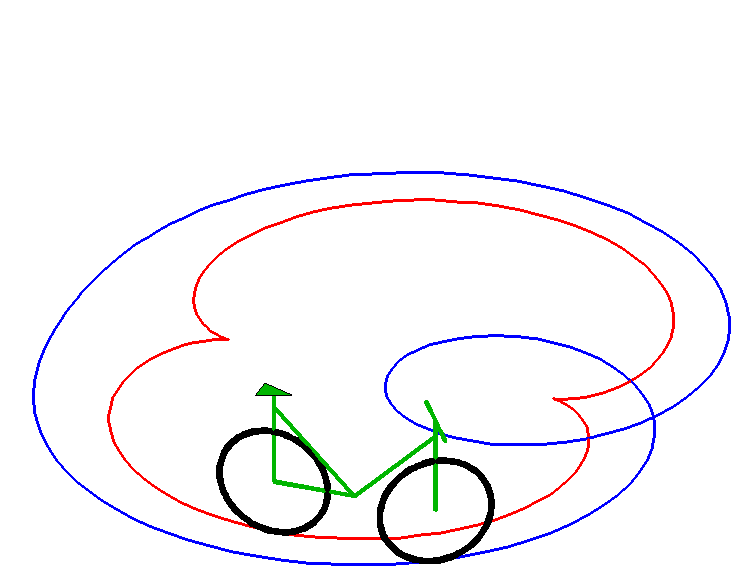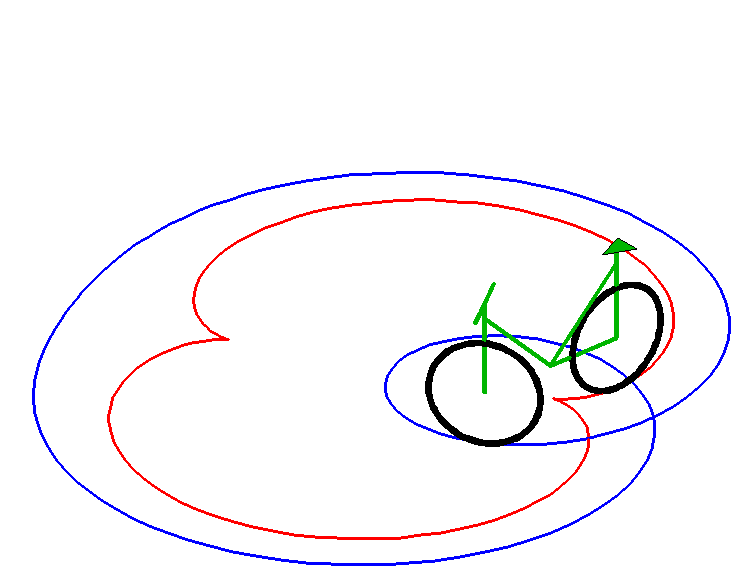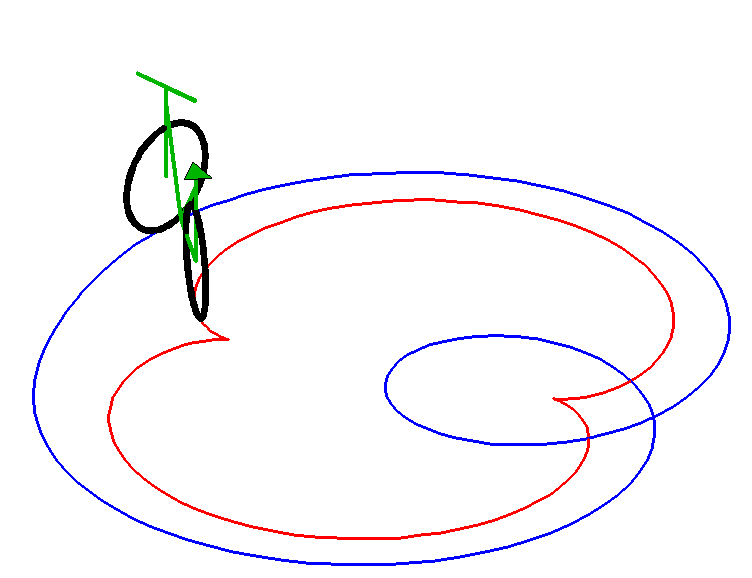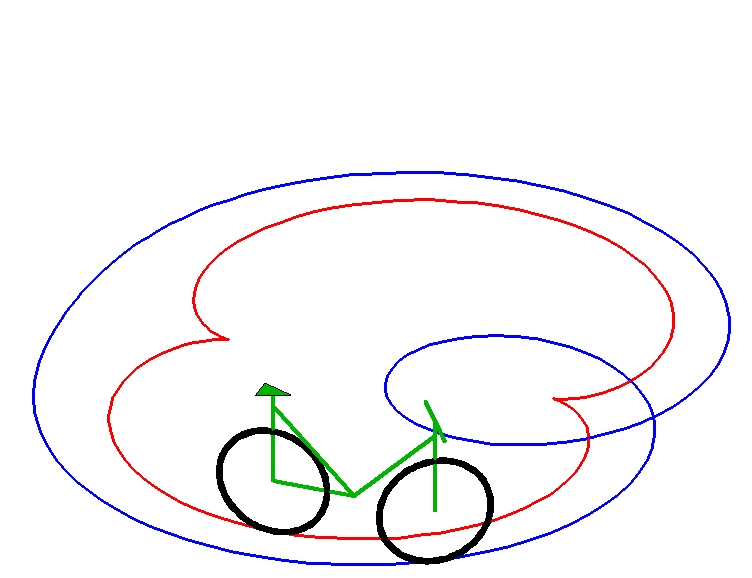
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017