Tractory of a circle

TRACTORY OF A CIRCLE

Curve studied by Bordoni in 1820.
Other name: tractrix of a circle.
Cycling animations by Alain Esculier, see more on his website.
See gomez texeira II p 94 , loria 2d p. 220 and loria 3d p. 82

Cartesian differential equation:

.
Polar differential equation:

where

.
Polar equation:
- Case 0 < a < R (leash smaller than the radius):
Inside branch:

Outside branch:

- Case a > R (leash larger than the radius):

See the definition at tractory.

When the length of the "leash" is equal to the radius of the circle, we get the tractrix spiral with asymptotic point at the centre of the circle.

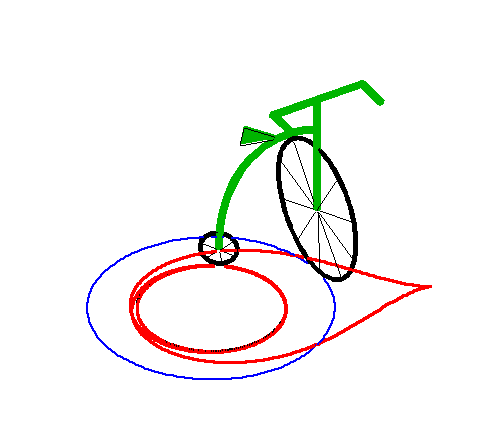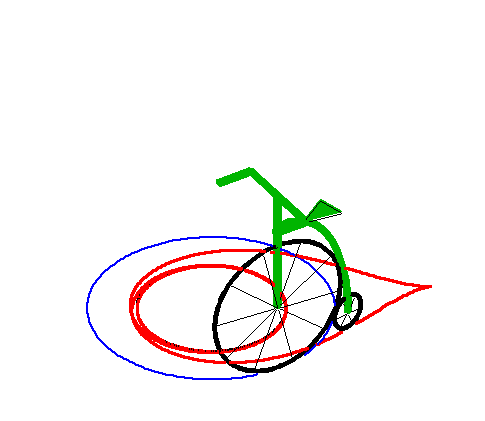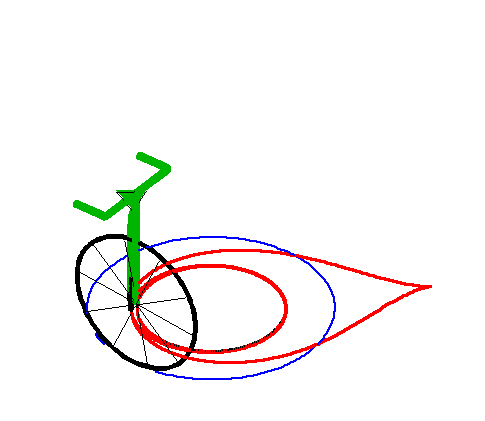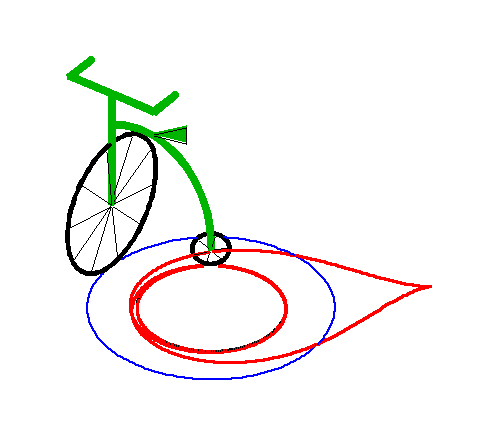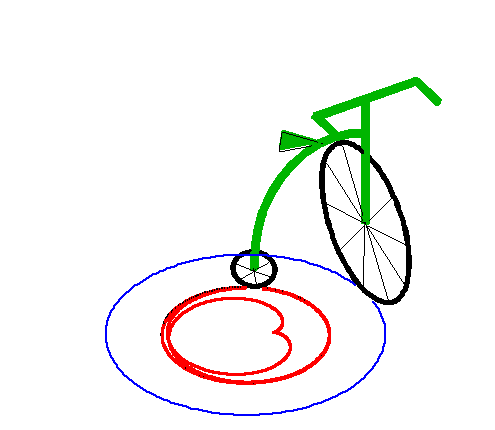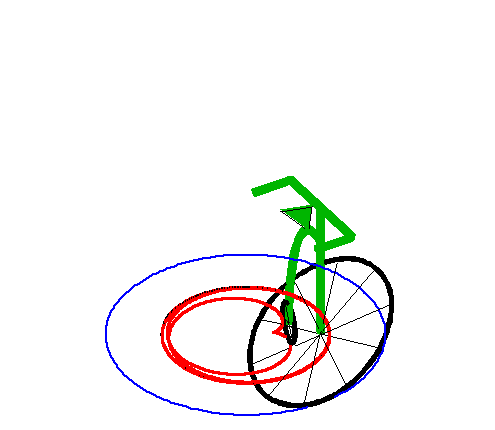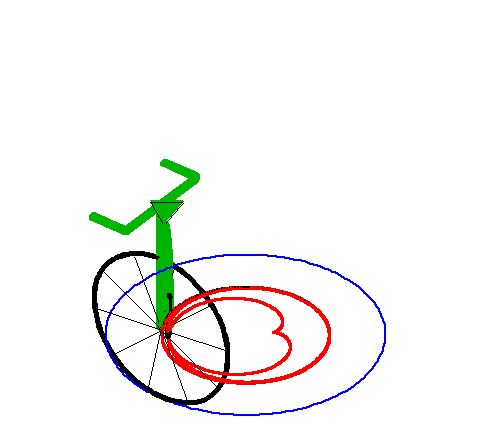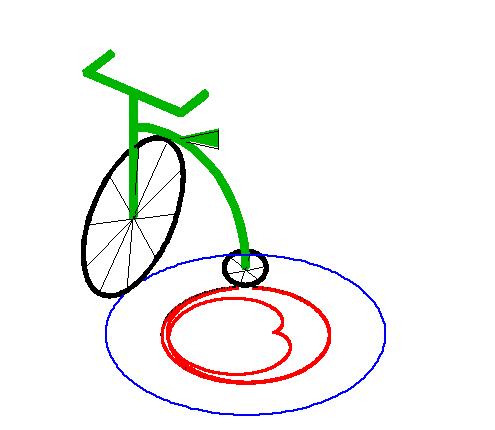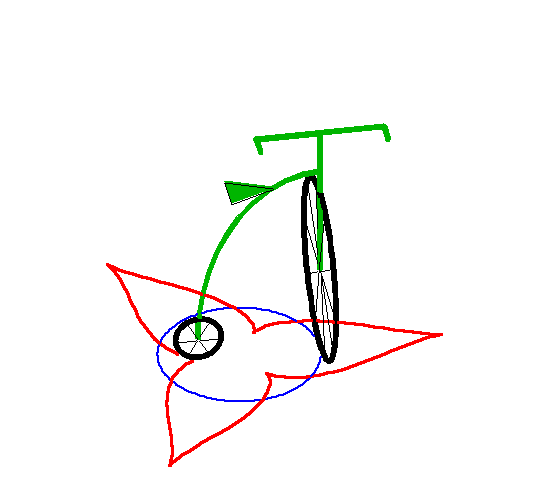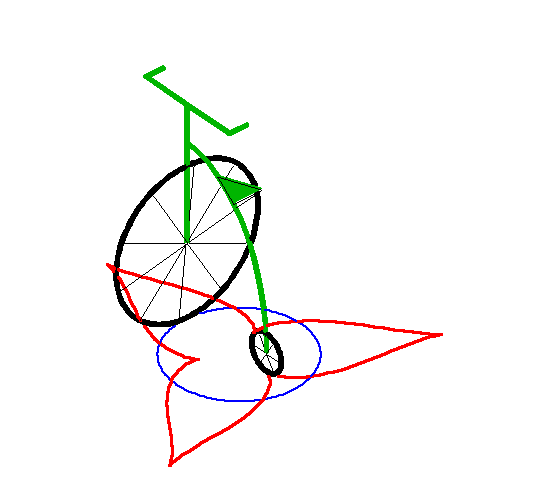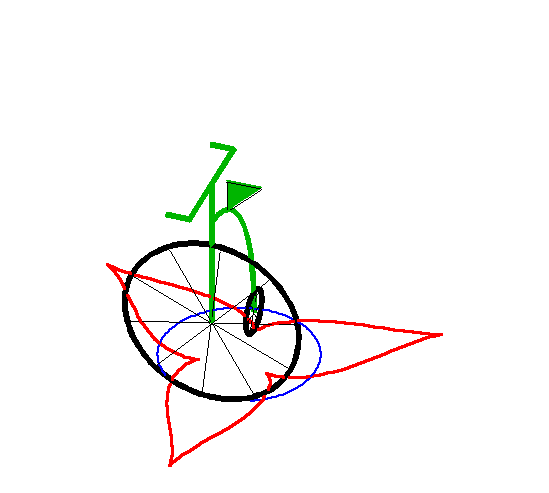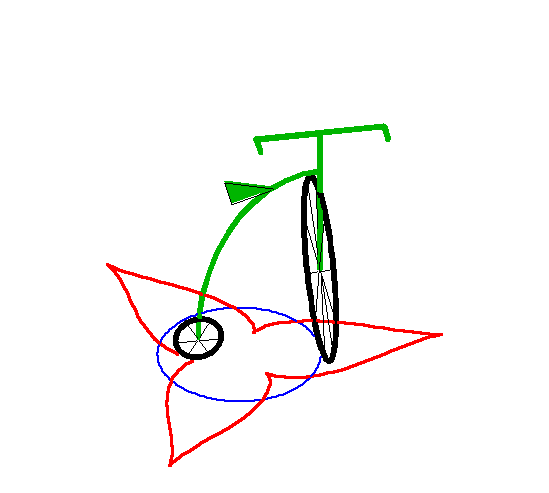
When the leash a is strictly smaller than the radius R of the circle, the curve has two branches for which the circle with radius is an asymptote; above, animation of the branch outside the asymptotic circle. Above, the inside branch.

This asymptotic circle is itself a special tractory, as illustrated on the right.
This corresponds to the case of a vehicle in motion with a fixed steering angle.

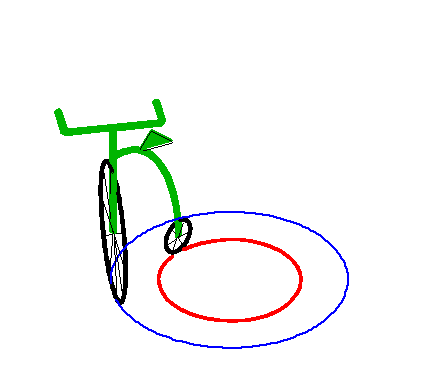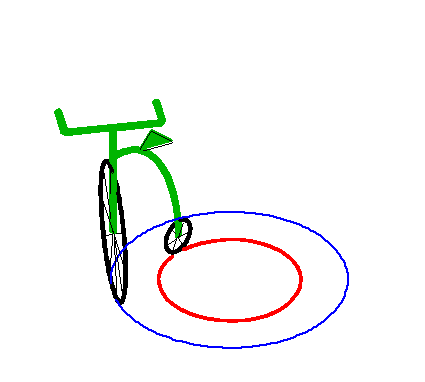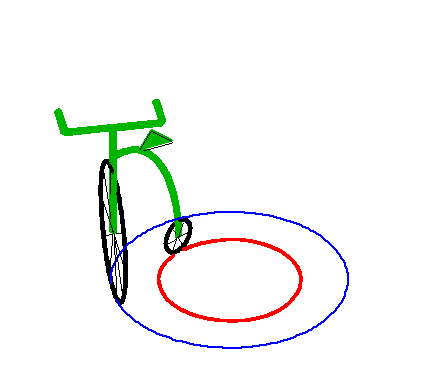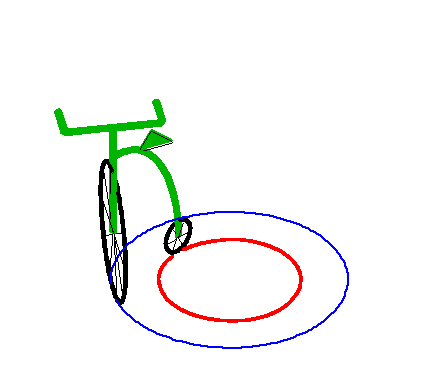When the leash is strictly greater than the radius of the circle, we get a curve with a series of cuspidal points.
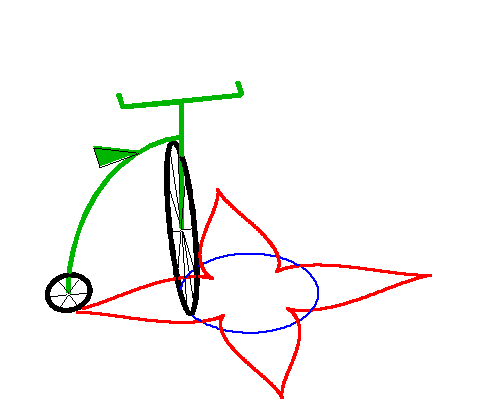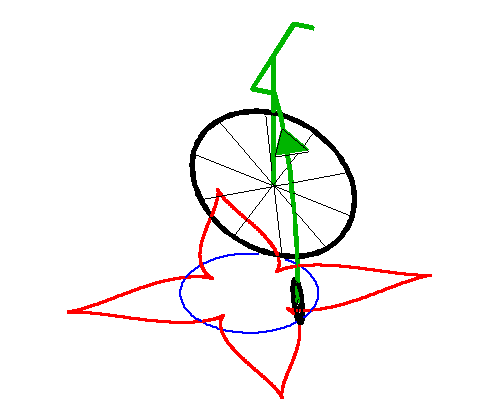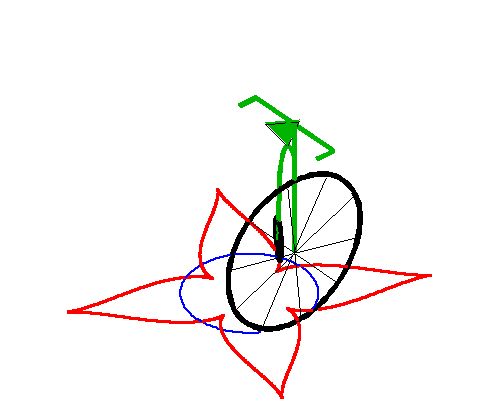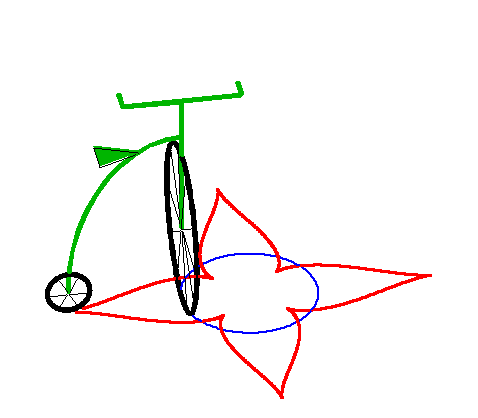This curve is closed iff is rational: see an example opposite, and two more at the top of the page.

If a tractory of a circle slides on a fixed line at a fixed point, then the pole of the tractory remains at constant distance from the end of the leash and therefore describes a circle; the tractories of circles are therefore a solution to the problem of the circular glissette (see a figure in the case of the tractrix spiral).
The evolutes of tractories of circles, which are polygasteroids, therefore are solutions to the problem of the circular roulette (see Catalan curve).

Look at www.cabri.net/abracadabri/Courbes/Tract/Tract2b.html

next curve previous curve 2D curves 3D curves surfaces fractals polyhedra


When the leash a is strictly smaller than the radius R of the circle, the curve has two branches for which the circle with radius is an asymptote; above, animation of the branch outside the asymptotic circle.	Above, the inside branch.
This asymptotic circle is itself a special tractory, as illustrated on the right. This corresponds to the case of a vehicle in motion with a fixed steering angle.
When the leash is strictly greater than the radius of the circle, we get a curve with a series of cuspidal points. This curve is closed iff is rational: see an example opposite, and two more at the top of the page.