Polygasteroid

POLYGASTEROID

Name given by Loria in 1930.
Other names: curve with n antinodes, or curve with n overhangs ( Laboulaye, 1849), generalized conic (Mamikon, 2012).

Polar equation: with positive n.
Algebraic curve iff n is rational.

The polygasteroids are the inverses of the conchoids of roses.
They also are the conical projections of cylindric sine waves on a plane perpendicular to the axis of the cylinder, when the centre is on the axis.

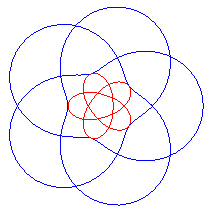
Conchoid of a rose in blue, polygasteroid in red

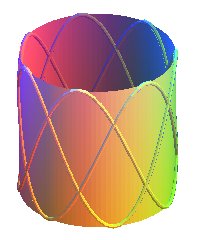Remark: the "monogasteroids" (n = 1) are none other than the conics. Therefore, the polygasteroids are the Brocard transforms of conics with respect to one of their poles.

The curve is composed of a base pattern symmetrical about Ox, obtained for :

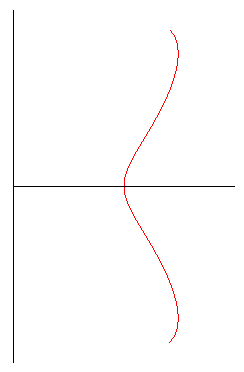
base pattern for e < 1
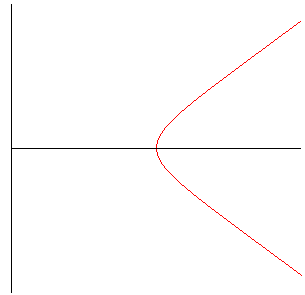
base pattern for e = 1
(parabolic branch)
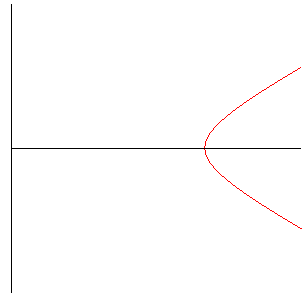
base pattern for e > 1
(branch with asymptotes)

transformed by all the rotations by , when k is an integer.
When n is rational and its numerator is p, p rotations generate the whole curve.

Case e < 1: we get shapes similar to inverse conchoids of roses.
For n = p / q, the polygasteroid with parameter n is one of the possible projection of the Turk's head knot of type (p,q); its p external vertices and its p internal vertices form a regular polygon, and it has p(q – 1) double points.

n = 1: ellipse
n = 2: Booth oval
n = 3
n = 4
n = 5

n = 1/2
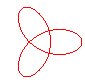
n = 3/2
projection of the trefoil knot
n = 5/2
projection of the 5.1 knot
n = 7/2
n = 9/2

n = 1/3
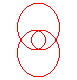
n = 2/3
projection of the eight knot
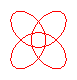
n = 4/3
projection of the 8.18 knot
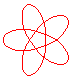
n = 5/3
projection of the 10.123 knot
n = 7/3

n = 1/4
n = 3/4
projection of the 9.40 knot
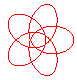
n = 5/4
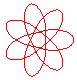
n = 7/4
n = 9/4

n = 1/5
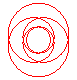
n = 2/5
n = 3/5
n = 4/5
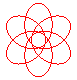
n = 6/5

These curves can be obtained as the mating profiles of ellipses.

Case e = 1 : equation becomes (compare to the epispirals).

n = 1: parabola
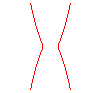
n = 2: Kampyle of Eudoxus
n = 3
n = 4
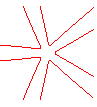
n = 5

n = 1/2
n = 3/2
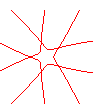
n = 5/2
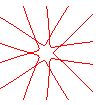
n = 7/2
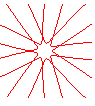
n = 9/2

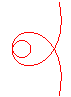
n = 1/3
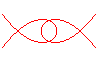
n = 2/3
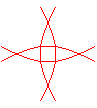
n = 4/3
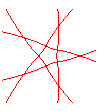
n = 5/3
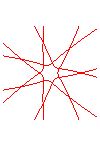
n = 7/3

n = 1/4
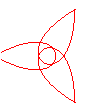
n = 3/4
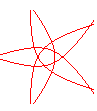
n = 5/4
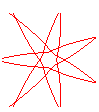
n = 7/4
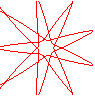
n = 9/4

n = 1/5
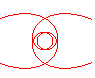
n = 2/5
n = 3/5
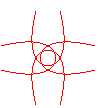
n = 4/5
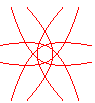
n = 6/5

Case e > 1:

n = 1: hyperbola
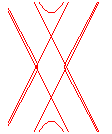
n = 2

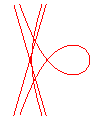
n = 1/2
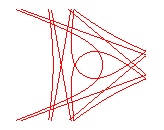
n = 3/4

The polygasteroids are the planar expansions of the planar section of the cone of revolution.

If the plane of the conic is winded into a cone with vertex O, half-angle at the vertex , and axis Oz, then the projection on xOy of this winded conic is the polygasteroid , which provides a construction of the latter in the case n < 1.

These curves can also be obtained as the mating profile of a line.

The evolutes of the tractories of circles as well as the projections on the symmetry plane of the rhumb lines of the open torus are polygasteroids.

next curve previous curve 2D curves 3D curves surfaces fractals polyhedra

n = 1: ellipse	n = 2: Booth oval	n = 3	n = 4	n = 5
n = 1/2	n = 3/2 projection of the trefoil knot	n = 5/2 projection of the 5.1 knot	n = 7/2	n = 9/2
n = 1/3	n = 2/3 projection of the eight knot	n = 4/3 projection of the 8.18 knot	n = 5/3 projection of the 10.123 knot	n = 7/3
n = 1/4	n = 3/4 projection of the 9.40 knot	n = 5/4	n = 7/4	n = 9/4
n = 1/5	n = 2/5	n = 3/5	n = 4/5	n = 6/5

n = 1: parabola	n = 2: Kampyle of Eudoxus	n = 3	n = 4	n = 5
n = 1/2	n = 3/2	n = 5/2	n = 7/2	n = 9/2
n = 1/3	n = 2/3	n = 4/3	n = 5/3	n = 7/3
n = 1/4	n = 3/4	n = 5/4	n = 7/4	n = 9/4
n = 1/5	n = 2/5	n = 3/5	n = 4/5	n = 6/5