Noeud de billard cylindrique

NOEUD ET ENTRELAC DE BILLARD CYLINDRIQUE, OU BONNET TURC
Cylindrical billiard knot and link or Turk's head knot, ZylinderBillardknoten und -Link oder türkischer Bund

Liens : wikipedia
www.mi.sanu.ac.rs/vismath/pennock/index.html
Images réalisées par Alain Esculier.

Un nœud de billard cylindrique, appelé comunément "bonnet turc", est le nœud obtenu à partir d'une trajectoire fermée d'une boule dans un billard cylindrique (boule non soumise à la pesanteur !), en modifiant les points de croisements en passages alternés dessus-dessous.

On parlera de nœud de type (p, q) (p et q premiers entre eux) si la boule fait p rebonds sur chaque bord et effectue q tours autour de l'axe (les spécialistes des nœuds marins parlent de bonnet turc à p ganses, ou boucles, et q spires, ou lignes ou encore torons). Lors d'un trajet entre deux rebonds, la courbe se coupe elle-même q – 1 fois : Il y a donc en tout p (q – 1) croisements.
Paramétrisation (portions d'hélices circulaires) : .
NB 1 : la notation anglo-saxonne pour le nombre q de tours est L, initiale de Lead (=interligne) et pour le nombre p de rebonds, c'est B initiale de Bight (=anse) ; le noeud (p,q) sera ainsi écrit : qL x pB.
NB 2 : si H est la hauteur du cylindre et D son diamètre, la longueur totale de la corde vaut ici .

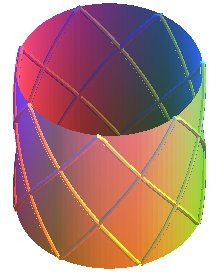
Ici, p = 7 et q =3 ; 7 rebonds par bord horizontal,
3-1 = 2 croisements par trajet entre deux bords.

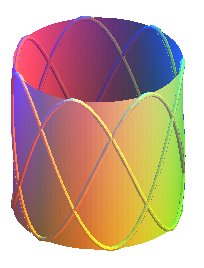
Le nœud de billard cylindrique de type (p,q) peut aussi s'obtenir par couronne sinusoïdale.
Paramétrisation :

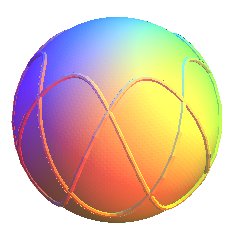
Par projection conique sur la sphère tangente, on obtient une sinusoïde sphérique : .

Par projection conique sur un plan perpendiculaire à l'axe, la couronne sinusoïdale s'aplanit en une polygastéroïde de paramétrisation : ;
si l'on projette la première version, les portions d'hélices circulaires se projettent en des portions de spirales hyperboliques :.

Par inversion, les courbes précédentes se transforment en conchoïde de rosace et en portions de spirales d'Archimède:
Paramétrisation :
et

Lorsque p > 2q, mais seulement dans ce cas, la courbe est topologiquement équivalente au polygone croisé ou polygramme de symbole de Schläfli {p/q} (p sommets reliés de q en q).

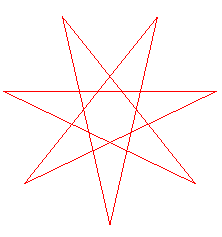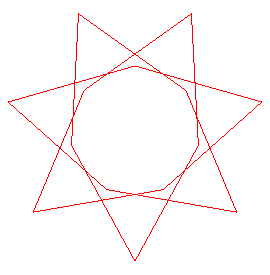A gauche, le cas (4, 3) a été alterné dessus-dessous.
Mais si, lors d'un trajet entre deux bord, on passe toujours dessus, et si, dans le trajet suivant, toujours dessous, on obtient un nœud torique, différent du nœud alterné dès que .

Exemples (pour q = 1, ou 2, se reporter aux noeuds toriques) :

p = 2 , q = 3 : noeud de huit

p = 4, q = 3 : nœud 8.1.18

p = 5, q = 3, nœud 10.1.123

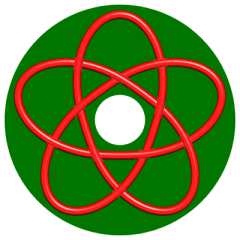p = 8, q = 3

Sculpture sur bois de J. Mandonnet

p = 3, q = 4 : nœud 9.1.40

p =5, q = 4 : 15 croisements

p =6, q = 5 : 24 croisements

p =5, q = 6 : 25 croisements

p = 11, q = 5 : 44 croisements

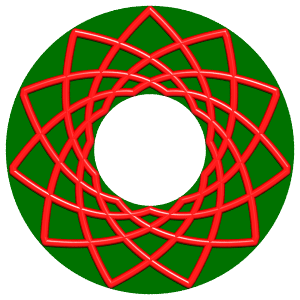Nota : le cas (n, n – 1) est équivalent au noeud de trèfle généralisé à n feuilles alterné.

Généralisation aux entrelacs.

Pour deux entiers > 0 p et q non premiers entre eux, posons d = pgcd(p, q), p' = p/d, q' = q/d ; la trajectoire de billard cylindrique de type (p', q') et ses d – 1 images par les rotations d'angle d'axe l'axe du cylindre, avec croisements alternés dessus-dessous forment un entrelac à d composantes, dénommé aussi bonnet turc de type (p, q).
Il y a toujours p (q – 1) croisements.
Comme on le verra sur les photos, ces entrelacs sont très prisés dans l'art islamique.

Pour q = 1 ou 2, l'entrelacs est équivalent à l'entrelacs torique de même type.

Assiette marocaine type (6,2) (plus trois boucles). Stuck d'artisanat marocain type (8, 2). Dessin d'Eric Broug, spécialiste des motifs islamiques type (12, 2).

Exemples avec :

Mosaïque romaine de la villa Casale, en Sicile : type (6, 3) ; entrelacs brunnien.
Enserré dans un (8, 2). Logo ChatGPT : on pourrait penser à un type (6, 3) à 3 boucles, non alterné, donc non brunnien ... ... Mais sous cette forme, c'est un (6, 2) alterné. Dessous de bouteille turc : type (12, 3) ; entrelacs brunnien également. Bois peint, Damas : type (16, 4) (photo Mohamed Roumi) Logo de la société européenne pour les mathématiques et les arts : type (12, 8), non alterné.

Remarque : si l'on autorise des croisements quelconques, et non seulement alternés, on obtient alors tous les nœuds possibles. En effet, tout nœud a une projection qui est un polygone régulier croisé.

Regarder aussi les noeuds polygonaux progressifs, qui sont équivalents aux bonnets turcs.
Ci-contre le bonnet de type (4,3).

Comparer avec les noeuds de billard rectangulaire.

Regarder aussi le graphe associé au bonnet turc de type (p,q) (qui possède p(q–1) arêtes), qui permet un tracé facile du bonnet en pratique.
Ci-contre les bonnets de type (5,3) et (5,4), et leur graphe à 10 et 15 arêtes.

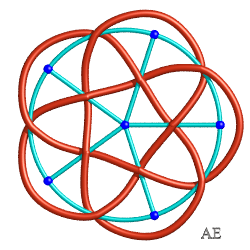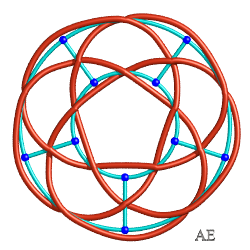Achetez des pendentifs en bonnets turcs : www.golden-knots.com/pendant.html

p = 10, q = 5
p = 9, q = 5
p = 10, q = 4 (artisanat de Guadeloupe)

courbe suivante courbe précédente courbes 2D courbes 3D surfaces fractals polyèdres

On parlera de nœud de type (p, q) (p et q premiers entre eux) si la boule fait p rebonds sur chaque bord et effectue q tours autour de l'axe (les spécialistes des nœuds marins parlent de bonnet turc à p ganses, ou boucles, et q spires, ou lignes ou encore torons). Lors d'un trajet entre deux rebonds, la courbe se coupe elle-même q – 1 fois : Il y a donc en tout p (q – 1) croisements. Paramétrisation (portions d'hélices circulaires) : . NB 1 : la notation anglo-saxonne pour le nombre q de tours est L, initiale de Lead (=interligne) et pour le nombre p de rebonds, c'est B initiale de Bight (=anse) ; le noeud (p,q) sera ainsi écrit : qL x pB. NB 2 : si H est la hauteur du cylindre et D son diamètre, la longueur totale de la corde vaut ici .	Ici, p = 7 et q =3 ; 7 rebonds par bord horizontal, 3-1 = 2 croisements par trajet entre deux bords.
Le nœud de billard cylindrique de type (p,q) peut aussi s'obtenir par couronne sinusoïdale. Paramétrisation :
Par projection conique sur la sphère tangente, on obtient une sinusoïde sphérique : .

Par projection conique sur un plan perpendiculaire à l'axe, la couronne sinusoïdale s'aplanit en une polygastéroïde de paramétrisation : ; si l'on projette la première version, les portions d'hélices circulaires se projettent en des portions de spirales hyperboliques :.
Par inversion, les courbes précédentes se transforment en conchoïde de rosace et en portions de spirales d'Archimède: Paramétrisation : et
Lorsque p > 2q, mais seulement dans ce cas, la courbe est topologiquement équivalente au polygone croisé ou polygramme de symbole de Schläfli {p/q} (p sommets reliés de q en q).


Assiette marocaine type (6,2) (plus trois boucles).	Stuck d'artisanat marocain type (8, 2).	Dessin d'Eric Broug, spécialiste des motifs islamiques type (12, 2).

Mosaïque romaine de la villa Casale, en Sicile : type (6, 3) ; entrelacs brunnien. Enserré dans un (8, 2).	Logo ChatGPT : on pourrait penser à un type (6, 3) à 3 boucles, non alterné, donc non brunnien ...	... Mais sous cette forme, c'est un (6, 2) alterné.	Dessous de bouteille turc : type (12, 3) ; entrelacs brunnien également.	Bois peint, Damas : type (16, 4) (photo Mohamed Roumi)	Logo de la société européenne pour les mathématiques et les arts : type (12, 8), non alterné.