Un noeud au sens mathématique peut être défini comme une classe d'équivalence de courbes lisses de  fermées sans auto-intersection, deux courbes étant équivalentes si on peut les déformer dans  continûment l'une en l'autre, la courbe restant constamment fermée sans auto-intersection tout au long de la transformation.
Le nombre de croisements d'un noeud est le nombre minimum de points doubles des projections planes sans point d'ordre supérieur ou égal à 3 de ses représentations. Le noeud dont une représentation est sans croisement est appelé noeud trivial, ou non-noeud.
 

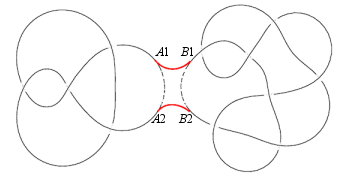
La somme de deux noeuds A et B étant le noeud obtenu en coupant A et B, faisant apparaître 4 extrémités A1, A2, B1, B2 et en recollant A1 avec B1, A2 avec B2 (le noeud obtenu ne dépendant pas du lieu des sections), on définit un noeud premier comme ne pouvant être somme de deux noeuds non triviaux, les autres (excepté le noeud trivial) étant dits composés, lesquels se décomposent de manière unique en somme de noeuds premiers.

Comme le montre le diagramme de droite, ce noeud se décompose en  un noeud de huit (4 croisements) et un noeud premier à 7 croisements 7.1.7.

Les six premiers sont des noeuds de bretzel.
Voir sur cette page le graphe associé au noeud.
Voir le noeud de trèfle 3.1.1, le noeud de huit 4.1.1, les noeuds plat et "de vache", le noeud de Carrick, le noeud d'arrimeur 6.1.1, le noeud carré 9.1.23, les noeuds toriques, polygrammiques, de billard rectangulaire ou cylindrique, polygonaux progressifs, de Lissajous et de billard 3D, celtiques linéaires.
Voir aussi les conchoïdes de rosace qui fournissent de nombreux noeuds à symétrie de rotation.

Voir enfin les entrelacs, ainsi que les surfaces de Seifert, surfaces ayant pour bord un noeud.
Comparer avec les courbes génériques.
 
 

	Noeud impossible par Oscar Reutersvärd. C'est un noeud premier de type 8.1.16.
	Noeud islamique à 16 croisements. Code de Gauss : 1,2,3,4,5,6,7,8,9,10,11,12,2,13,4,14,6,15,8,16,10,1,12,3,13,5,14,7,15,9,16,11
	Joli non-noeud ! Opticien à Vienne.

Autres liens sur les noeuds :
Livre de Peter Cromwell
Knot-atlas
Applette java permettant de retrouver le code de Gauss d'un noeud à partir de son tracé :  knotilus.math.uwo.ca/javasketch.php
Site permettant de retrouver un noeud premier à partir de son code de Gauss : knotilus.math.uwo.ca
www.knotplot.com/download pour télécharger le magnifique logiciel de Robert Charein : "knotplot".
 
 
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL   2019