KNOT

Prime knot with 19 crossings
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
KNOT

Prime knot with 19 crossings
A knot, in the mathematical sense, can be defined as an
equivalence class of smooth curves of
closed without self-intersection, two curves being equivalent if one can
be transformed into the other in
continuously, the curve remaining closed and without self-intersection
throughout the transformation.
The crossing number of a knot is the minimal number of
double points of the planar projections of its representations that do
not have points of order greater than or equal to 3. The knot that has
a representation without crossings is called trivial knot, or unknot.
| The sum of two knots A and B is defined as the knot obtained by cutting A and B, calling the four ends A1, A2, B1, B2 and glueing A1 to B1, and A2 to B2 (the resulting knot does not depend on where the cuts were made). A prime knot is a knot that cannot be the sum of two non trivial knots. Other knots (except the trivial one) are called composite knots, and can be written in a unique way as the sum of prime knots. |
 As the diagram on the right shows, this knot can be decomposed into
|
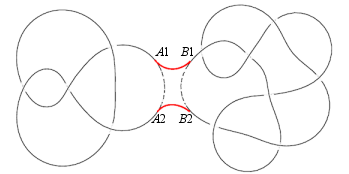 |
Here are the diagrams of the prime knots with from 0 to
9 crossings:

(see also this
link)
The first six are Pretzel
knots.
See on this
page the graph associated to the knot.
See the trefoil knot 3.1.1,
the figure-eight knot 4.1.1, the square
and granny knots, the
Carrick bend,
the stevedore knot 6.1.1, the
toric
knots, the
polygram knots,
the rectangular or
cylindrical
billiard knots, the
polygonal knots,
the
Lissajous and 3D billiard
knots, the linear Celtic knots.
See also the conchoids
of roses that provide many knots with rotation symmetry.
Finally, see the links,
as well as the Seifert
surfaces, surfaces the edges of which are a knot.
Compare to the generic
curves.
 |
Impossible knot by Oscar Reutersvärd.
It is a prime knot of type 8.1.16. |
 |
Islamic knot; 16 crossings.
Gauss code: 1,2,3,4,5,6,7,8,9,10,11,12,2,13,4,14,6,15,8,16,10,1,12,3,13,5,14,7,15,9,16,11 |
Other links on knots:
Book
by Peter Cromwell
Knot-atlas
Java applet to determine the Gauss
code of a knot from its drawing: knotilus.math.uwo.ca/javasketch.php
Website that allows to recover a prime knot from its Gauss
code: knotilus.math.uwo.ca
www.knotplot.com/download
to download Robert Charein's magnificent software: "knotplot".
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2018