next curve previous curve 2D curves 3D curves surfaces fractals polyhedra

FIGURE-EIGHT KNOT

The figure-eight knot is the only knot with 4 crossings (more precisely, the crossing number of which is equal to 4).
As opposed to the trefoil knot, it is reflexive (equal to its image by reflection).
 
The rope knot which, by connecting the two free blades, gives the mathematical figure-eight knot is indeed shaped like an eight.
However, the opposite knot is equivalent to the figure-eight knot; therefore, it could also have been called "heart knot"!

Here are, in order, the equations of the first 4 representations in the header:
Homemade representation based on a lemniscate of Gerono developed in space, the ends then being connected by a Bézier curve.

Cartesian parametrization: 

 Paul Bourke's representation, based on an epitrochoid with q = 2 and k = 5 .
Cartesian parametrization:
.
 Rohit Chaudhary's representation: 

Representation based on a trochoid with d/R = 6, connected by an arch of ellipse. Representation based on the cylindrical sine wave

 
One of the geodesic line of the oblate spheroid forms an elegant 3D representation of the figure-eight knot, with axis of symmetry.

 
Opposite, drawings by G. K. Francis (a topological picture book) showing the passages between the various representations of the figure-eight knot.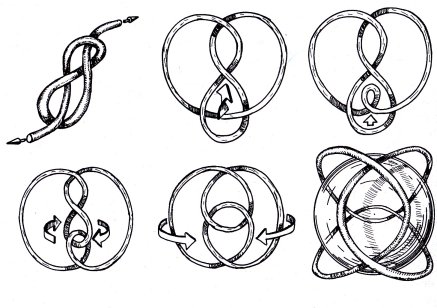

The figure-eight knot is one of the "Turk's heads".
See also the associated Seifert surface.
See more details on the website knot atlas.
 
 

Figure-eight knot by Alain Esculier

Figure-eight knot on a stained-glass of the Chateau de Blois.
Symbol of the link between the kingdom of France and the duchy of Brittany.


Mongolian frieze: infinite sum of figure-eight knots (Batsukh Bold, Mongolian national ornaments).


next curve previous curve 2D curves 3D curves surfaces fractals polyhedra

© Robert FERRÉOL 2020