TREFOIL KNOT
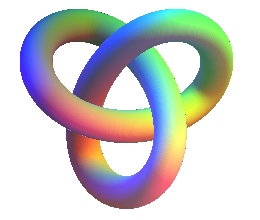
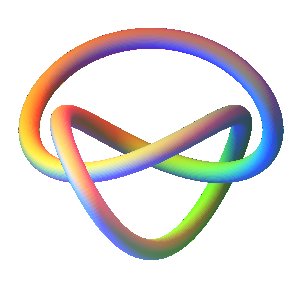
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
TREFOIL KNOT
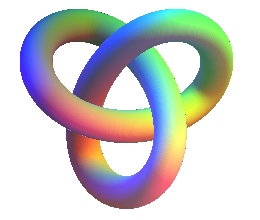
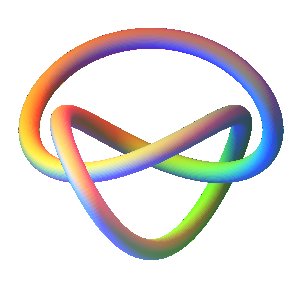
| Websites:
Knot atlas etacar.put.poznan.pl/piotr.pieranski/IdealKnots.html |
 |
Cartesian representation for which the projection on
xOy
is a hypotrochoid: |
 |
Representation by a toric
solenoid with coefficient n = 3/2: |
 |
Other representation: 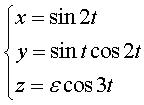 . .
See also here an open trefoil knot. |
The trefoil knot is the only knot for which the crossing number is minimal, namely 3; there are in fact two of them, they are enantiomorphic (images of one another by reflection).
It is an overhand
knot:  the ends of which were connected.
the ends of which were connected.
The trefoil knot is also the torus knot of type (3,2) (3 coils around the torus, on two turns), as well as that of type (2,3):

torus knot with 3 coils on 2 turns |
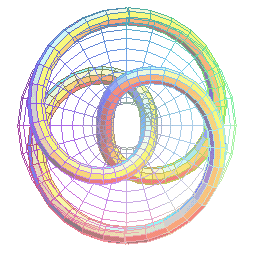
torus knot with 2 coils on 3 turns; contrary to what it looks like, we get a trefoil knot and not the figure-eight knot. |
| The trefoil knot is the edge of a Möbius strip with 3 half-twists. |
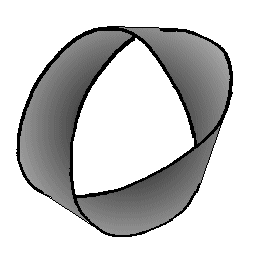 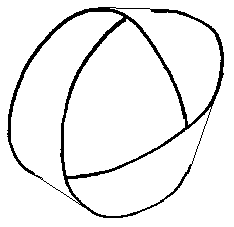 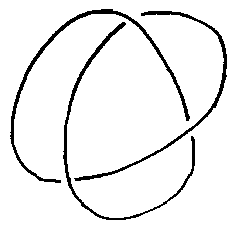 |
| Conversely, a strip knotted as a trefoil knot yields a Möbius strip with 3 half-twists: |  |
| Trefoil knot from a folded strip.
The strip has 6 half-turns, and therefore it is not a Möbius strip (it has two faces, and two edges). (Logo of Point gamma, student party of Polytechnique). |
 |
| Opposite, a trefoil knot obtained by a closed skew polygonal line with six segment lines; though it might seem, the 7 bars do not have the same lengths (the 3 external bars are shorter). |
 |
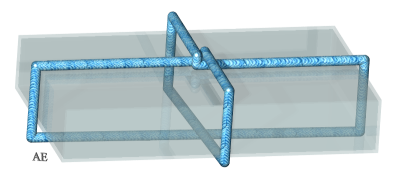
Opposite, a trefoil knot obtained with 6 segment lines of the same
length;
the coordinates of the 6 points a,b,c,d,e,f are: [[-1, 0, 0], [1, 0, 0], [(13-4*22^(1/2))/25, 6/5, -(4/25)*(-1+22^(1/2))*3^(1/2)], [-1/2, 3/5, (1/2)*3^(1/2)], [1/2, 3/5, -(1/2)*3^(1/2)], [(-13+4*22^(1/2))/25, 6/5, (4/25)*(-1+22^(1/2))*3^(1/2)], [-1, 0, 0]]: |
|
| It has been proved that it is impossible to obtain a trefoil knot with 5 bars, except in the opposite impossible figure (idea of Alain Esculier, in the style of Oscar Reutersvärd.). |  |
For 6 bars, it is also impossible for the segment lines to be pairwise parallel, except again for this impossible figure | 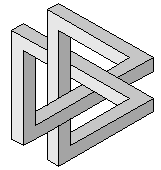 |
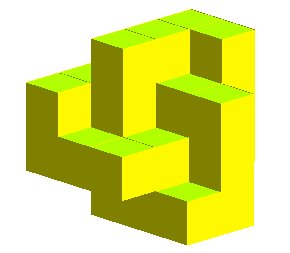
| Opposite, several views of a trefoil knot composed of
polygonal lines with right angles.
It can be proved that this figure represents the smallest trefoil knot passing by the vertices of a cubic lattice. |
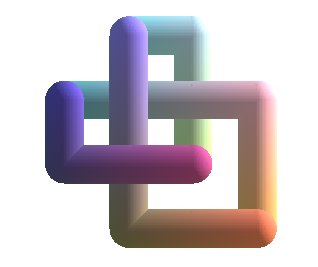 |
 |
 |
| Two other polygonal versions with 9 and 12 segment lines. |  |
 |
| The name "trefoil knot" is probably due to the resemblance of the opposite representations to a trefoil leaf: |
 |
 |
| This knot with 4 visible crossings is a trefoil knot
(turn the top loop to make the central crossing disappear).
Inverse the two top (or bottom) crossings and you get a figure-eight knot. |
 |
| The string of this package form a trefoil knot (but, if a crossing is inverted, the knot becomes trivial). |
 |
| This Mongolian ornament type motif forms a trefoil knot (one crossing can be removed). |
 |
| We could call "4-leaf trefoil knot" the curve for which
the projection on xOy is a hypotrochoid
with 4 leaves, parametrized by: |
 |
| This can be generalized to the "n-leaf trefoil
knot": |
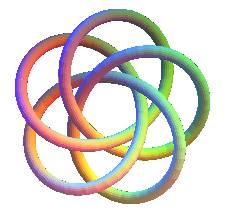 |
See also the two graphs associated to the trefoil knot, the Seifert surface associated to the trefoil knot, the square and granny knot, sums of two trefoil knots.
The trefoil knot in art:
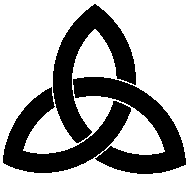 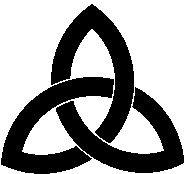
The simple Celtic knot is a trefoil knot |
  |

The trefoil knot as seen by Escher |

Sculpture of a trefoil knot, university of Flensburg
|
The trefoil knot is often used as a logo:
 |
|
 |
 |
||
|

Behind the logo Woolmark, one can imagine a trefoil knot... |
 |
 |
|
Celtic trefoil knot interlaced
with a trivial knot.
|

Logo of the Cimat,
center for research in mathematics of Guanajuato, Mexico.
|

Alien trefoil knot! |
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2018