Link

LINK

Other name: interlacing.
Reference:
Dale Rolfsen, Knots and Links (1976).

A link is a finite set of interlaced knots. More precisely, it is an equivalence class of finite sets of closed curves of without double points nor common points, two sets of curves being equivalent if each curve of one set can be continuously transformed in into a curve of the other set, the curve remaining closed and without double points nor common points with any other curve along the transformation.

The crossing number of a link is the minimal number of double points in the planar projections (without points of order greater than or equal to 3) of its representatives. A link a representative of which has a projection without crossings is said to be trivial.

Given two blades in two links, the corresponding sum of the two links is the link obtained by cutting the blade chosen in each link and glueing the edges. A prime link is a link that cannot be the sum of two non trivial links.

Here is the Rolfsen table of the first prime links, with two or more blades (the symbol gives the crossing number N, the number of blades n, and the order number p among the links with N crossings):

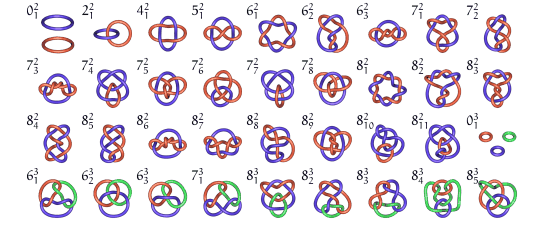
The first six are Pretzel links.
See also the graph that enables to encode each link.
More complete table in the knot atlas.

Examples, with the notation N.n.p (N = crossing number, n = number of blades, p = order number given by Rolfsen):

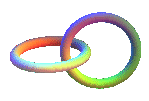The simplest of links: the Hopf 2.2.1link, that is also the toric solenoid of type (2, 2); the sum of n Hopf links gives a link with n + 1 rings like the link of the Olympic Games.
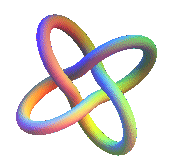Link 4.2.1or Solomon's knot that is also the toric link of type (4, 2).

Whitehead link 5.2.1
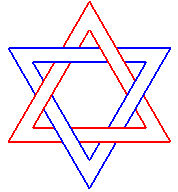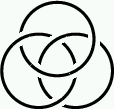
Link 6.2.1or seal of Solomon (not to be mistaken for the knot!), interlaced polygramm {6/2} or toric link (6, 2).

Borromean ring 6.3.2
False Borromean rings: the first one is none other than a Hopf link with three rings (that is not even a prime link) et the second one is the 6.3.3 (each ring is interlaced with all the others).

See also the Carrick bend, Brunnian links, that become trivial when we get rid of one of the components, billiard links, the Turk's heads, Pretzel links, linear celtic knots, the link of the icosidodecahedron, the Seifert surfaces, that fill a link, Antoine's necklace, that is the limit of a sequence of links.

Notice that the weave on the left is in fact a trivial link. By the way, it is the reason why it can be made with crepe paper without tearing it!

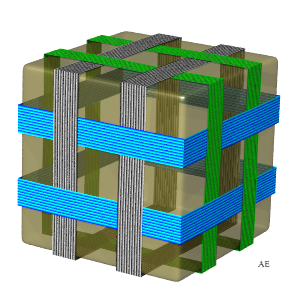This cube strapping forms an link of 6 loops end 24 crossings that is linked to the rhombicuboctahedron.
On the right, two flat versions of the same link; notice the symmetry of order
4 for one, and 3 for the other one.

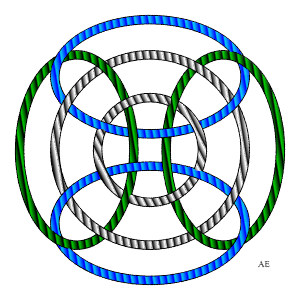Web links:
List of prime links : katlas.org/wiki/The_Thistlethwaite_Link_Table
Java applet that determines the Gauss code of a link from its drawing: knotilus.math.uwo.ca/javasketch.php
Website that finds a prime link from its Gauss code: knotilus.math.uwo.ca
Christian Mercat's website, to learn to create your own links www.entrelacs.net
Geraud Bousquet's software to draw links from a graph
www.math.utk.edu/~morwen/index.html
www.clanbadge.com/knots.htm
stained glass window in the Aubazine abbey
mathouriste.canalblog.com

next curve previous curve 2D curves 3D curves surfaces fractals polyhedra

The simplest of links: the Hopf 2.2.1link, that is also the toric solenoid of type (2, 2); the sum of n Hopf links gives a link with n + 1 rings like the link of the Olympic Games.	Link 4.2.1or Solomon's knot that is also the toric link of type (4, 2).
Whitehead link 5.2.1	Link 6.2.1or seal of Solomon (not to be mistaken for the knot!), interlaced polygramm {6/2} or toric link (6, 2).
Borromean ring 6.3.2	False Borromean rings: the first one is none other than a Hopf link with three rings (that is not even a prime link) et the second one is the 6.3.3 (each ring is interlaced with all the others).