
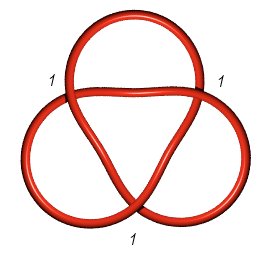
A P(1,1,1)

A P(3,-2,-2,2) made by Sandjer, pastry chef at Bretzel Love.
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
PRETZEL KNOT, LINK

A P(1,1,1) |

A P(3,-2,-2,2) made by Sandjer, pastry chef at Bretzel Love. |
| Wikipedia |
| If we call "tangle of order p" the intertwining of two circular helices with |p| crossings, turning counter-clockwise if p > 0 and clockwise otherwise, then the Pretzel link P( |
 |
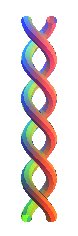 Tangle of order -5 |
 composed of two blades. |
| Pretzel links can also be characterized by the fact that their associated graph has n vertices placed on a circle with a series of multiple edges of orders For example, the blue graph opposite is associated to P(3,2,2). |
 |
The number of blades is equal to the number of even , if at least one of them is even. If all the
are odd, then there are one or two blades depending on whether n is odd or even.
If all the are positive, then the link has
alternating crossings.
The first six prime knots can be seen as Pretzel links with positive coefficients:
| Trefoil knot 3.1.1: P(1,1,1) or P(a,b), a+b=3 | Figure-eight knot 4.1.1: P(2,1,1) | Knot 5.1.1: P(1,1,1,1,1) or P(a,b), a+b=5 |
 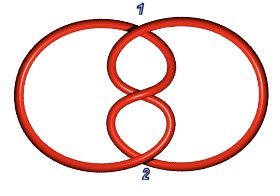 |
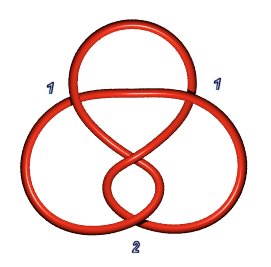 |
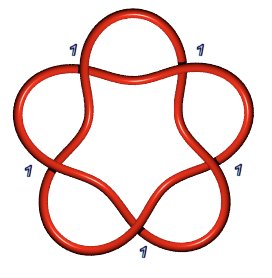
  |
|
|
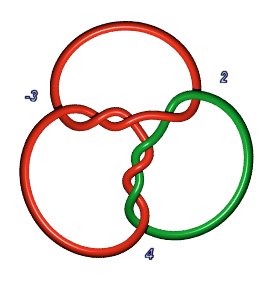
Stevedore knot 6.1.1: P(2,1,1,1,1) or P(4,1,1) | Knot 6.1.2: P(3,2,1) |
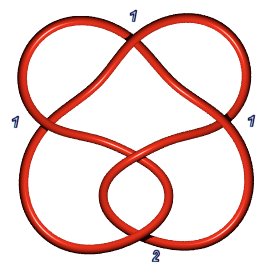
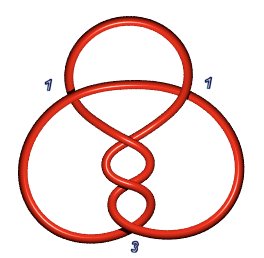 |
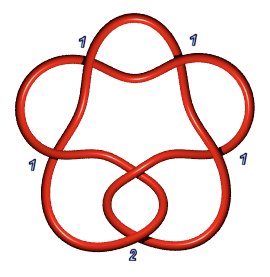
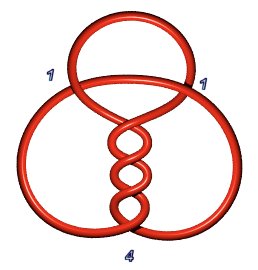 |
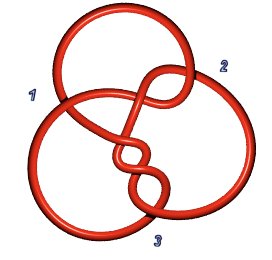 |
But this does not hold for the following one (6.1.3): .
For odd values of n, the Pretzel knot P(1,1,...,1) with n "1" is equivalent to the torus knot T(n,2).
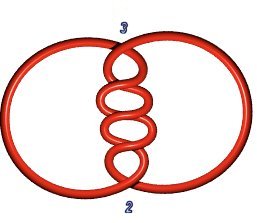
The first six prime links can also be obtained as Pretzel links with positive coefficients:
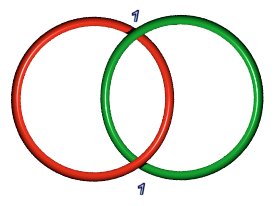
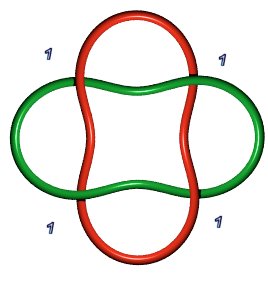
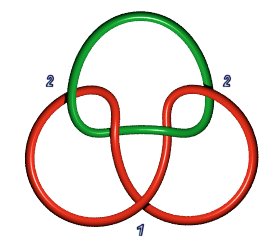
| Hopf link 2.2.1: P(1,1) | Solomon's knot 4.2.1: P(1,1,1,1) or P(2,2) or P(a,b), a+b = 4 | Whitehead link 5.2.1: P(1,2,2) |
 |
 |
 |
|
|
|
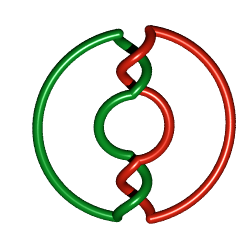
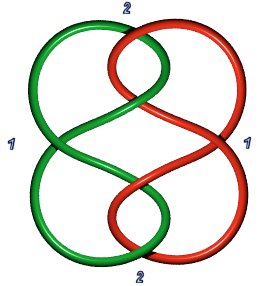
Solomon 's seal 6.2.1: P(1,1,1,1,1,1) or P(a,b), a+b=6 |
 |
 |
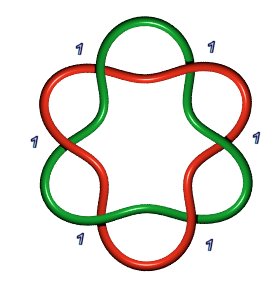
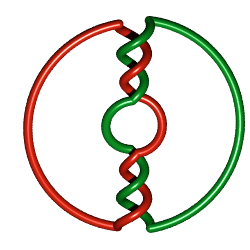 |
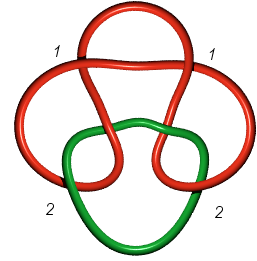
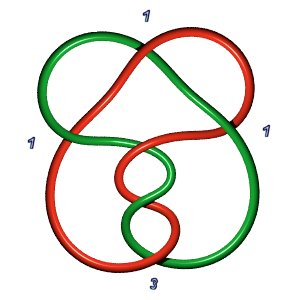
The link 6.3.2
(Borromean rings) is not a Pretzel link, but 6.3.1 is P(2,2,2): 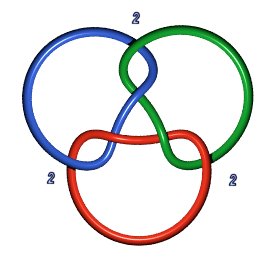
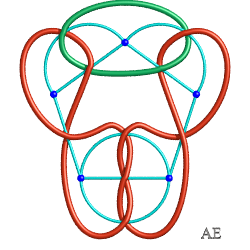
| When some of the The third view displays the link P(2,–3,–3) that has eight visible crossings and for which 8 is indeed the minimal number of crossings, see the 8.1.19 page. |
 |
.png) |
 |

A real Alsatian Pretzel!
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL
2018