EPITROCHOID
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
EPITROCHOID


| From the Greek epi "over" and trokhos "wheel".
Applet for tracing epitrochoids: www.wordsmith.org/~anu/java/spirograph.html |
| Complex parametrization: Cartesian parametrization: Polar parametrization: Area encompassed by the curve in the case |
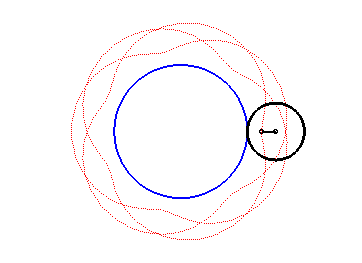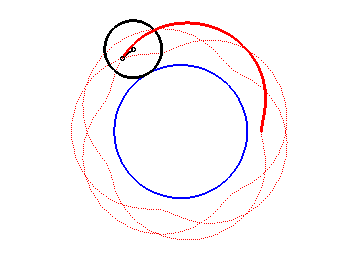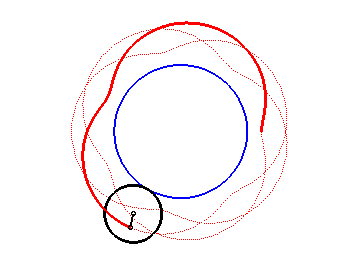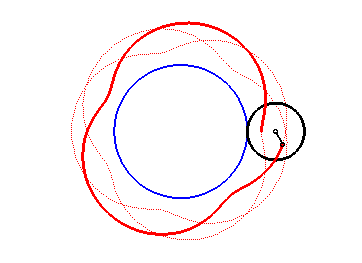
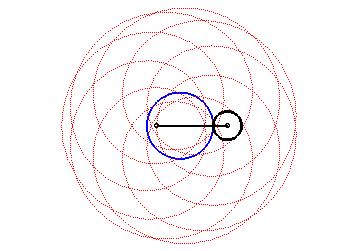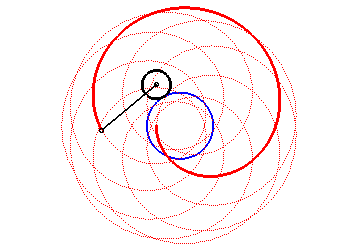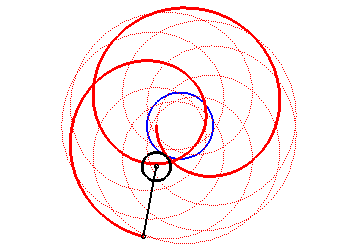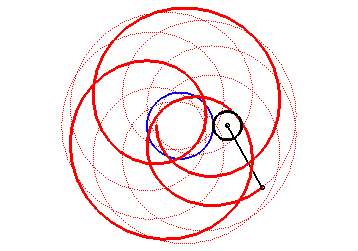
| The epitrochoids are the curves described by a point linked to a circle (C) rolling without slipping on a base circle (C0), the open disks with boundaries (C) and (C0) being disjoint; they are the curves obtained with a Spirograph with an external disk. |  |
In other words, they are also the roulettes of the movement of a plane over a fixed plane the base of which is a circle and the rolling curve of which is a circle outside the first one.
For d = b, i.e. k = 1, we get the
epicycloids.
For d = a + b, we get the roses.
For k < 1, the curve is also called shortened
epicycloid.
For k > 1, the curve is also called elongated
epicycloid.
| Every epitrochoid is also a peritrochoid
(property called "of double generation"): fixed circle with radius |
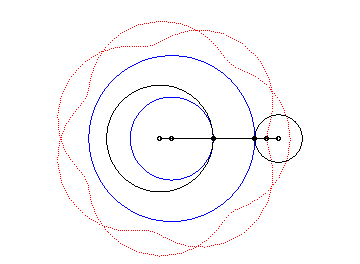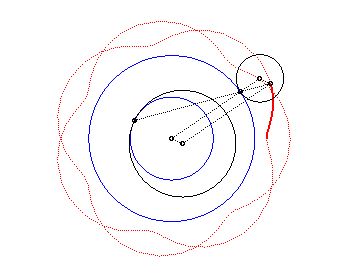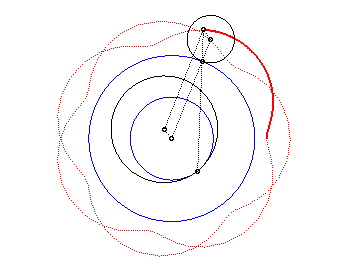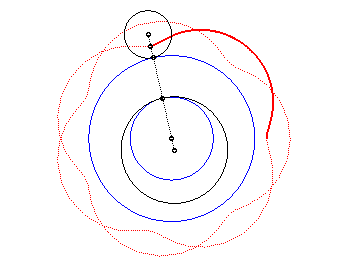 |
Here are the different shapes depending on the values
of k.
| It is remarkable that for From this paper, this is the case of the trajectory of the moon relative to the sun, for which Note that for the right trochoide, there are always changes in concavity. |
|
| The limit case is |
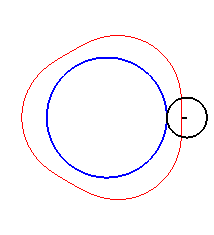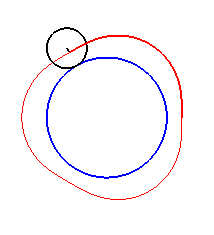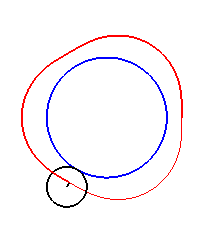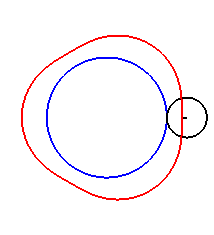 |
| For |
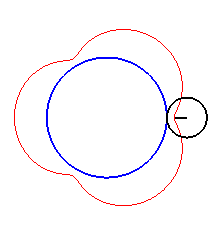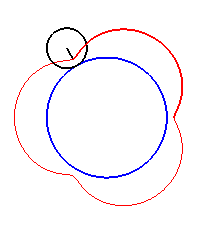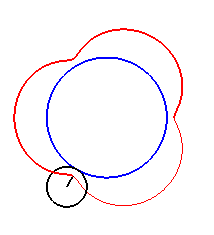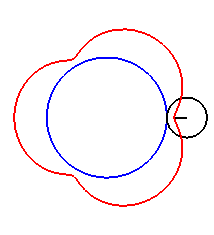 |
| For k = 1, we obtain the epicycloid, with cusps. |
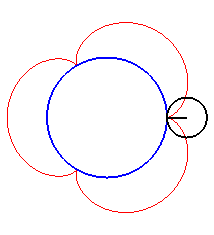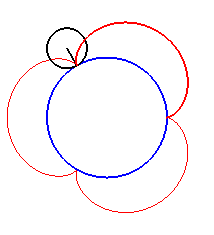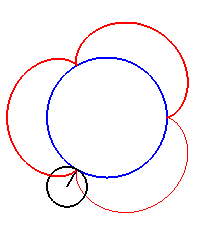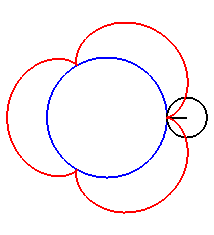 |
| For alternately). |
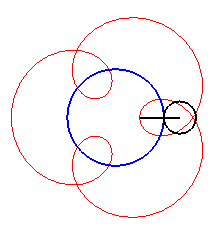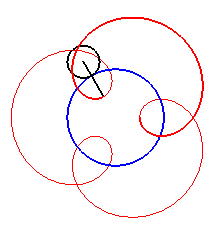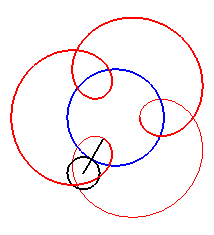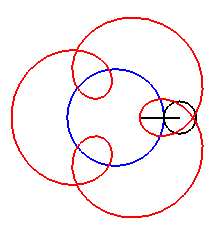 |
| For k = q + 1 (so d = a
+ b)), We get a rose with index
n
< 1 , of polar equation |
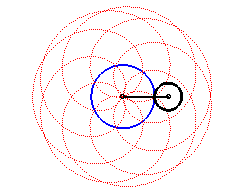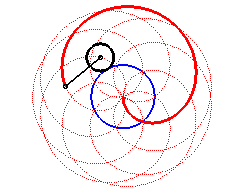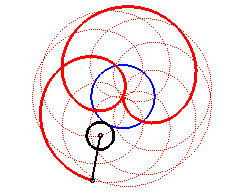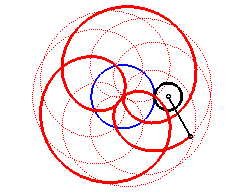 |
| Case k > q – 1. |
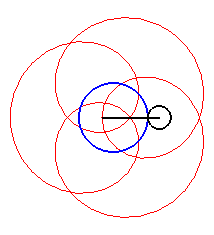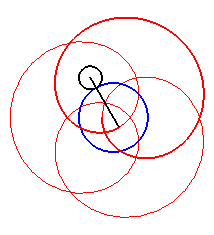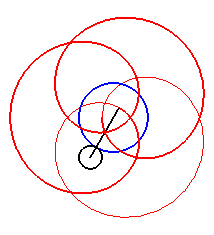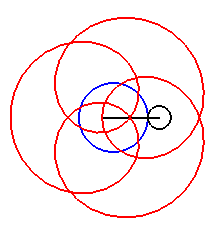 |
| Epitrochoids can also be defined by the trajectories
of a movement composed of two circular motions in the same direction and
different angular speeds, with complex parametrization: |
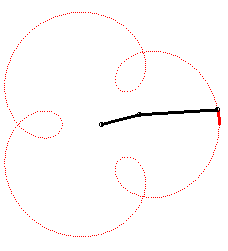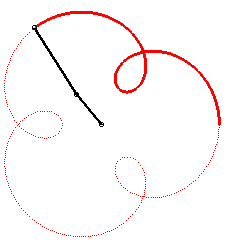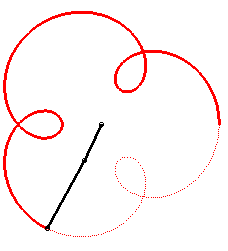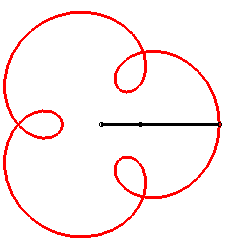
The angular speed (with respect to the fixed plane) of the first arm is the quadruple of that of the second arm: we get an epitrochoid with parameter q = 4 - 1 = 3. |
| Writing |
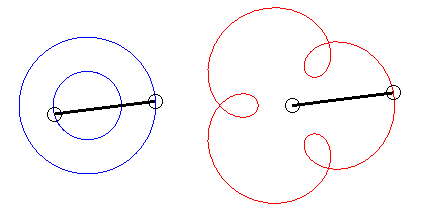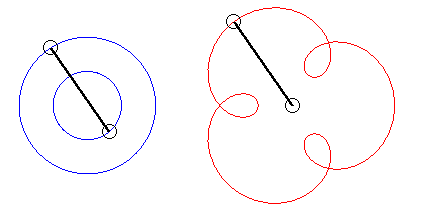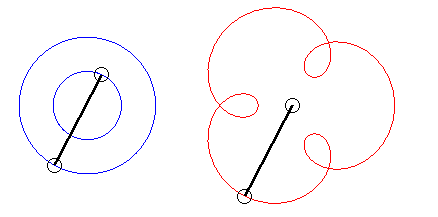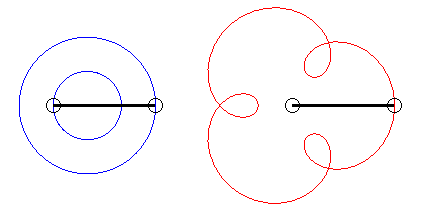 |
| Approximating the movements of the planets around the
Sun by coplanar uniform circular movements, we can consider that the visible
trajectories of the planets with respect to one another are epitrochoids.
These trajectories were called epicycles
(see also this
animation).
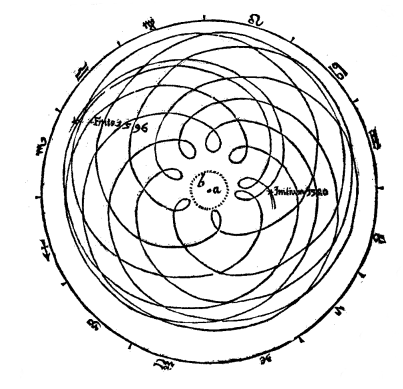
Opposite, a sketch drawn by Kepler in Astronomia nova, representing the evolution of the laces of the orbit of Mars from the Earth. |
 |
Shape of the curves in the different cases:
|
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
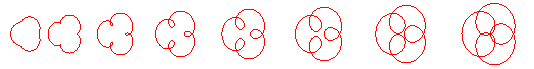 |
|
|
|
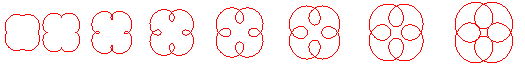 |
|
|
|
 |
|
|
|
 |
|
|
|
 |
The epitrochoids are also the plane projections of the Capareda curve, or the satellite curves, as well as the curves of constant precession.
The epitrochoids along with the hypotrochoids
are the centred trochoids
(see also a generalisation on this page).
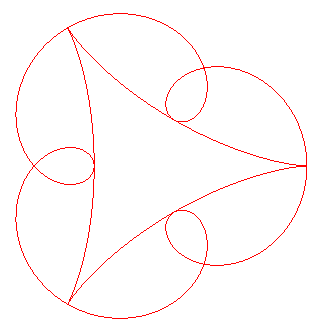
| Given a hypocycloid
with parameter |
 |
 |
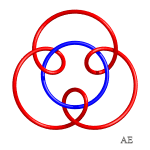
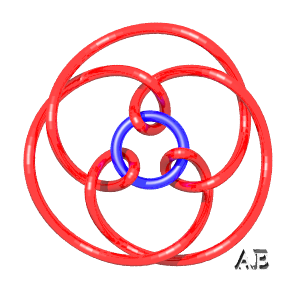
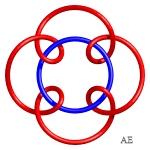
Here are various epitrochoids represented in 3D and then tied:
 |
 |
 |
 |
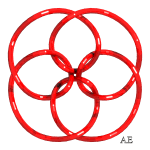
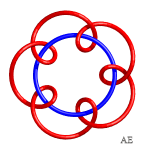
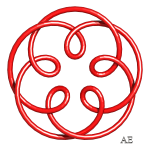
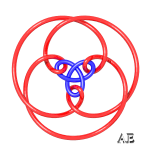
| q = 3, link 9.2.24 | q = 3, knot 9.1.40 | q = 3/2, link with 12 crossings | q = 4, see this page |
 |
 |
 |
 |
| q = 4, knot with 12 crossings | q = 5, link with 15 crossings | q = 5/2, knot 5.1.1 | q = 3/2 and q =3 intertwined, link with 15 crossings |
| Gear belt, in the form of an epitrochoid by Lévi Capareda during a class of industrial sciences... | 
|
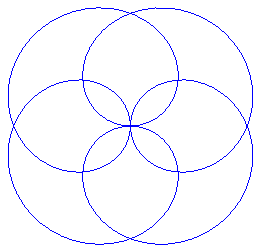 |

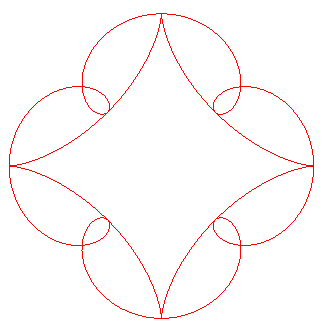
p = 4, k = 4 |
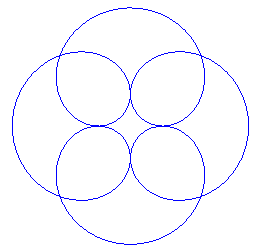 |
| Ditto with q = 2 (Dürer folium) | 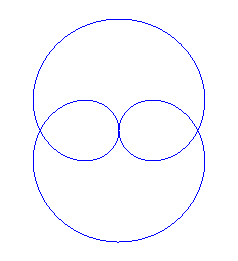 |
 |
| This pattern of an Arab tapestry has the same structure than the epitrochoid with p = 8, k = 5 (rotate by 1/16th of a turn). |
 |
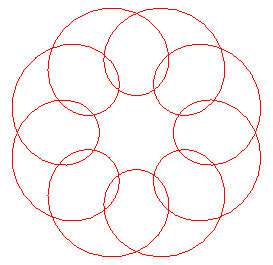 |
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017