Equidistance curve

EQUIDISTANCE CURVE, SYMMETRY SET, SKELETON

Other names: mediatrix, central curve, medial axis.
See the CAPES "exam" paper 1986 for the notion of dividing line.
Wikipedia articles: topological skeleton, medial axis.
Maple program for the skeleton of a convex polygon

Obtaining the equation of the equidistance curve: eliminate

from

The equidistance curve between two curves and is the locus of the points M located on a normal at M₁ to and on a normal at M₂ to with MM₁ =MM₂ . Therefore, it is also the locus of the centres of the circles tangent to both curves.
The curves and are thus symmetric about the equidistance curve.

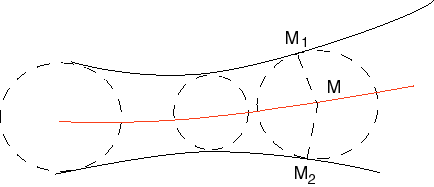The equidistance curve is the indecision curve of Buridan's ass!

Examples:
    - the equidistance curve of two parallel curves is yet another parallel curve.
    - the equidistance curve of two curves symmetric about a line is a portion of that line (for example, the equidistance curve of two secant lines is composed of the two bisectors).
    - the equidistance curve of the envelope of a family of circles and itself is the locus of the centre of the circles.
    - the equidistance curve of a curve and a point is the isotel of this curve with respect to this point.
    - the equidistance curve of a circle and a line is composed of one or two parabolas; writing F the centre of the circle, R its radius, D the line, then the equidistance curve is defined by where H is the projection of M on D. The focus of the parabola(s) is F and their directrix is parallel to D.

Various cases: disjoint, tangent, or secant circle and line.

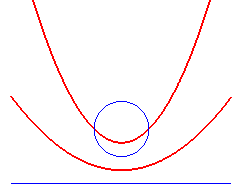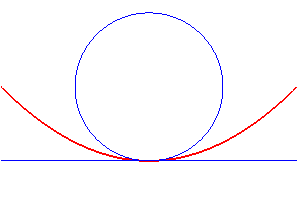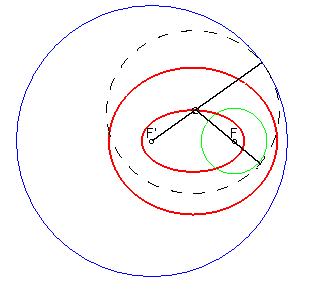
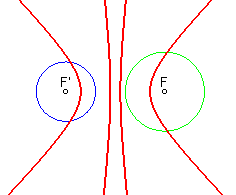
- the equidistance curve of two circles is composed of two bifocal conics; Writing (centre,radius) of the circles as (F,R) and (F',R') respectively, the equidistance curve is defined by ; and in space, these two conics are focal curves of two Dupin cyclids with the two circles as directrix circles.
These two conics are...

...two ellipses when one of the circles is inside the other: ...an ellipse and a line when one of the circle is inside the other and tangent to it: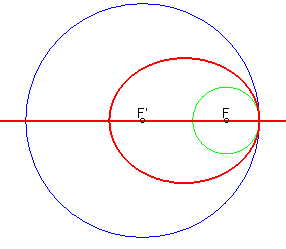

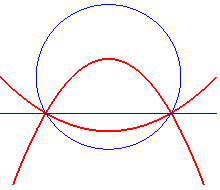
...an ellipse and a hyperbola when the circles are secant: ...an ellipse and a hyperbola when the circles are tangent and outside one another: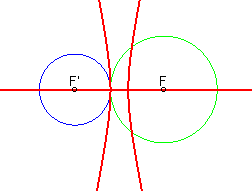

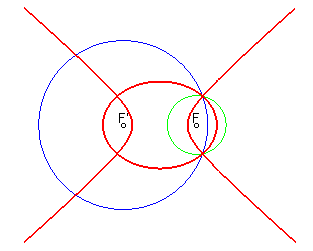
...two hyperbolas when the circles are outside one another: Opposite, the equidistance curve of a line and a parabola.
Algebraic curve of degree 6.

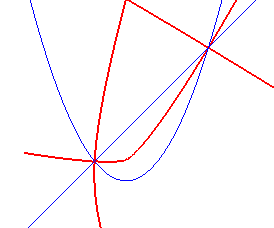The equidistance curve of the nephroid and the segment line joining the cusps is a circle.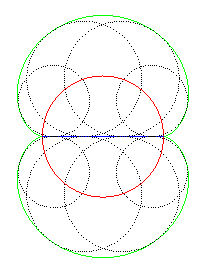

Let us consider the cases when the two curves coincide. The equidistance curve, which is then called symmetry set, is the locus of the centres of the circles bitangent (or multitangent) to the curve, and therefore also the locus of the points where the parallel curves intersect themselves.

Examples (initial curves in green, parallel curves in blue, skeleton in red, evolute in black).

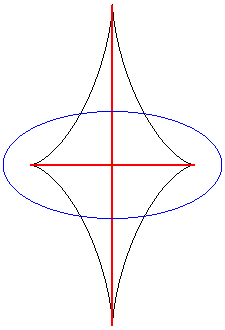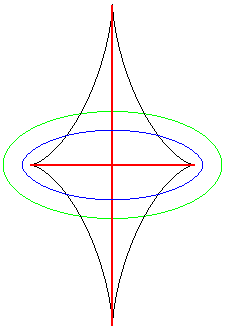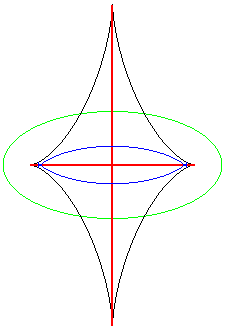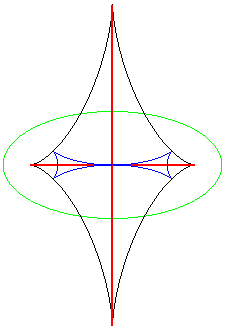
The symmetry set of an ellipse is composed of the two segment lines joining 2 cusps of its evolute, and reduces to the centre in the case of a circle.
It is easily seen on this animation that the equidistance curve is the locus of the double points of the parallel curves (toroids), the evolute being the locus of the cuspidal points. Symmetry set of a cardioid, locus of the double points of the parallel curves. Symmetry set of a bifolium (to imagine, looking at the locus of the doubles points of the parallel curves...)

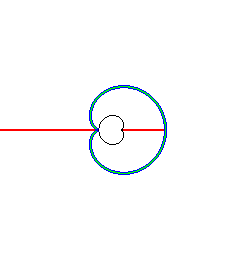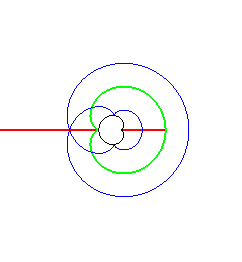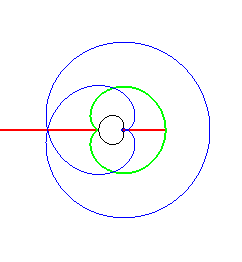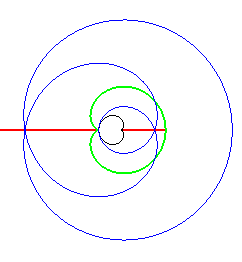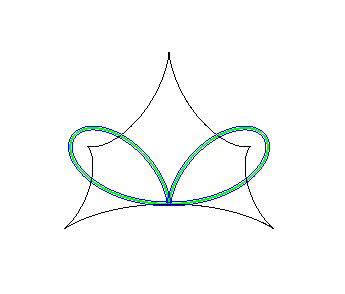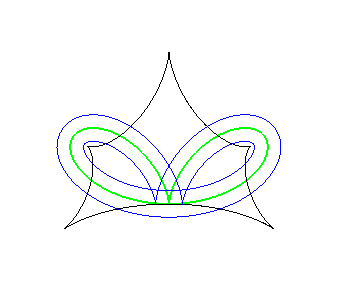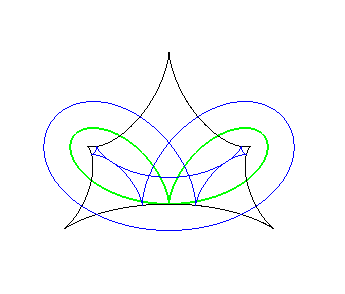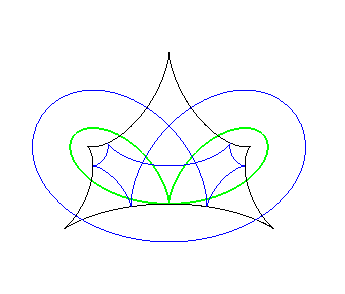The symmetry set of the envelope of a family of circles is the locus of the centres (but, be careful, some circles may have an imaginary contact with the curve: their centre will not be counted in the real skeleton); for example, the symmetry set of an anallagmatic curve is its deferent.

As for the parallel curves (cf. the distance lines), the notion of mediatrix of two parts of the plane is similar to that of equidistance curve. It is the set of points at equal distance from the two parts (the distance to a set being the infimum of the distances to a point in said set); when the two parts are curves, the mediatrix curve is in general included in the equidistance curve.
Here is, for example, the mediatrix curve of two secant circles, always composed of an ellipse, but the hyperbola of which has only one branch:

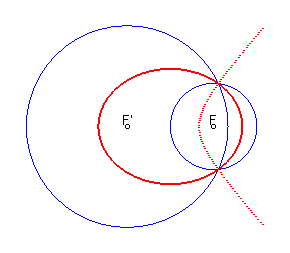
A generalisation is the notion of dividing line, where the distances are no longer equal but their ratio is given. For example, the Apollonius circles are the dividing lines of two points, the conics are the dividing lines of a line and a point, the Cartesian ovals are the dividing lines of two circles.

Dividing lines of two circles, defined by

.
In green for k > 1, in blue for 0 < k < 1 (Cartesian ovals), in red for k = 1 (branch of a hyperbola, mediatrix of two circles).

The notion similar to that of symmetry set is the skeleton of a compact part X of the plane, which is the closure of the set of centres of the maximal disks contained in the part (a maximal disk is a disk that is not included in any other disk).

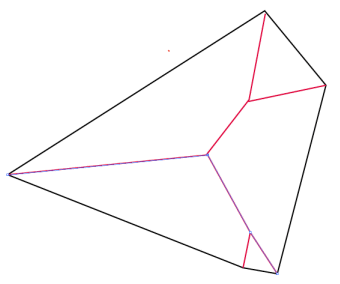
For example, the skeleton of a full triangle is composed of the interior bisectors, limited to the summits and the centre of the inscribed circle.

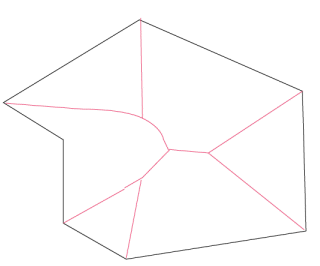
For a full convex polygon, the skeleton is composed of portions of bisectors of couples of sides, delimiting the "attraction zones" of each side (locus of the points closer to this side than to the others).
In the non-convex case, the skeleton also has portions of parabolas.

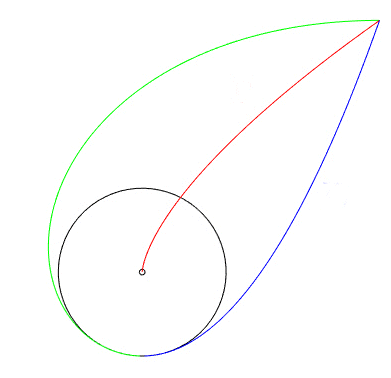
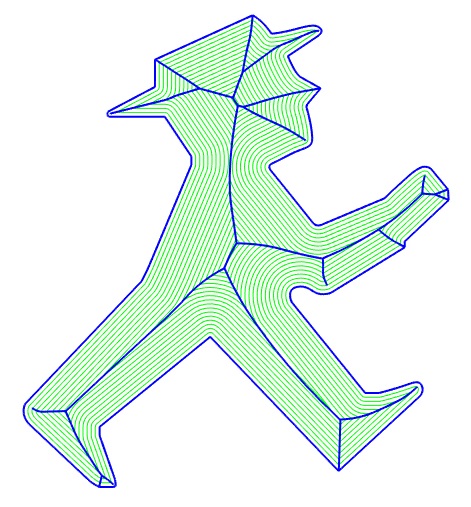
If the boundary is piecewise C¹, then the skeleton is a tree the extremities of which are the outgoing sharp points or the centres of curvature at the outgoing summits of the boundary.
Image on the left: arc of a parabola in blue, evolute of the symmetrical arc in red, symmetrical image of the blue arc about the red arc in green; the red arc is therefore the skeleton of the reunion of the green and blue arcs.
Image on the right designed by Robert March from the Berliner Ampelmännchen.

About skeletons, see also the sand piles, the crest of which is projected on the skeleton.

The notion can be extended to the case where X is any part; for example, if X is the complement of a finite part Y, the skeleton is composed of the boundaries of the Voronoi cells associated to the points of this set.

Compare to the median curve of two curves.

next curve previous curve 2D curves 3D curves surfaces fractals polyhedra

...two ellipses when one of the circles is inside the other:		...an ellipse and a line when one of the circle is inside the other and tangent to it:
...an ellipse and a hyperbola when the circles are secant:		...an ellipse and a hyperbola when the circles are tangent and outside one another:
...two hyperbolas when the circles are outside one another:		Opposite, the equidistance curve of a line and a parabola. Algebraic curve of degree 6.

The symmetry set of an ellipse is composed of the two segment lines joining 2 cusps of its evolute, and reduces to the centre in the case of a circle. It is easily seen on this animation that the equidistance curve is the locus of the double points of the parallel curves (toroids), the evolute being the locus of the cuspidal points.	Symmetry set of a cardioid, locus of the double points of the parallel curves.	Symmetry set of a bifolium (to imagine, looking at the locus of the doubles points of the parallel curves...)