Polar equation: r = R. Cartesian equation:  . Conic. Cartesian parametrization:   (). Rational Cartesian parametrization:   (). Curvilinear abscissa: . Tangential polar angle: . Radius of curvature, intrinsic equation 1: . Intrinsic equation 2:   (here  ) General Cartesian equation:  (not empty iff ) Cartesian equation of the circle with centre  and radius R:  . Cartesian parametrization: . Polar equation: , or  that reduces to  if the circle passes through O. Length: 2pR; area: .

A circle is the locus of the points at equal distance from a fixed point. It can be defined as "circular conic" or "non-degenerate conic with zero eccentricity", or "curve with constant curvature and zero torsion".

The curves with constant normal (N = const., cf. notations) are the circles with centre on Ox (and the lines parallel to Ox).

Given two distinct points A and B, the locus of the points M such that the angle between the lines MA and MB is constant is a circle for which [AB] is a chord (isoptic of the segment line [AB]).
 

The locus of the points M satisfying  is (except when k = 1) the circle (called "of Apollonius") with diameter [I J] where I and J are the two points on (AB) such that ; the lines (MI) and (MJ) are the bisectors of the angle AMB. The points A and B are inverses of one another with respect to this circle. Therefore, the circle of Apollonius also is the locus of the points M seeing the segment lines [AI] and [BI] with the same angle ((MA,MI)=(MI,MB)); the same holds for [AJ] and [BJ]. See this website. NB: do not mistake this for the Apollonius circles associated to 3 circles (see below).
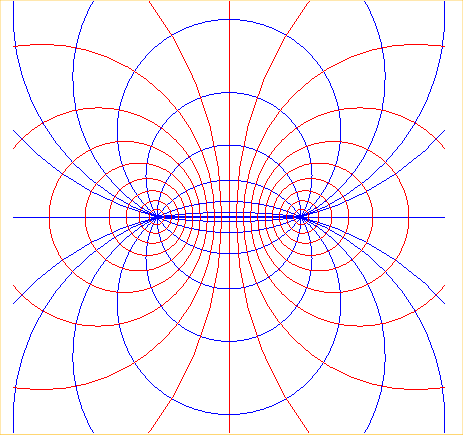
When k varies, these circles form a pencil of circles with limit points A and B; the conjugate pencil is the set of all circles passing through A and B (called "intersecting pencil", A and B being the intersection points) and each pencil is the set of all the circles orthogonal to one of the circles of the other pencil. This figure can be interpreted as the electrostatic or magnetic field lines; see here. See also the interference patterns for circular waves on the page conics.
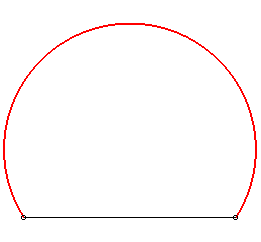
The circle also is the solution of the isoperimetric problem: finding the simple closed curve of given length that encloses the maximal area (or of minimal length for a given area). Similarly, the arc of a curve of given length L, joining two given points A and B, traced on a half-plane delimited by (AB), and enclosing the largest area in this half-plane is one of the two arcs of a circle of length L joining A and B (to be checked: if one looks for the area for which the gravity centre is the furthest from (AB), the answer now is an arc of a catenary).

 
 

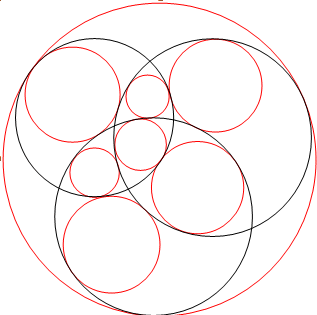
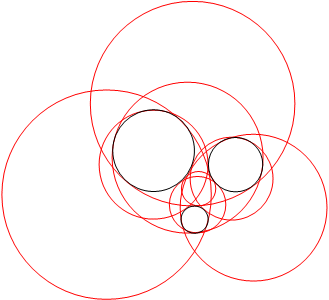
Another famous problem concerning circles, already posed by Apollonius, is that of determining the circles tangent to 3 given circles. In general, they are 8 solutions as in the examples opposite, but only 2 when the 3 circles are tangent to one another (see Apollonian gasket).

 

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL  2017