Since the orthotomic is the image of the pedal by a homothety with centre O and ratio 2, the isotel is none other than the image of the negative pedal by a homothety with centre O and ratio 1/2; the notion therefore became obsolete.
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
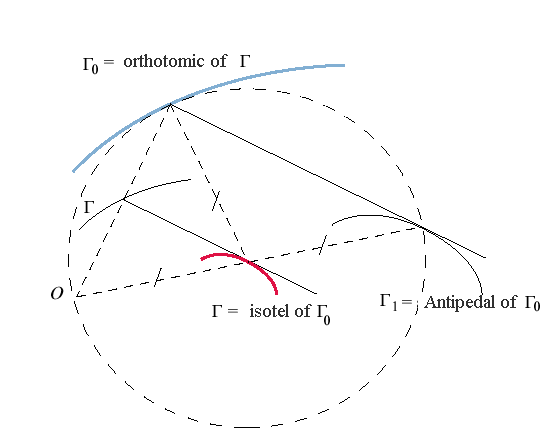
ISOTEL CURVE
| Notion studied by Lepiney in 1909.
From the Greek iso "same" and têle "far away". |
| The isotel curve of a plane curve (G0)
with respect to a point O is the locus of the points located at
equal distance from O and (G0),
in other words, the equidistance
curve of (G0)
and
O. If M0 describes
(G0), then the
isotel curve is the locus of the intersection points between the perpendicular
bisector of [OM0] and the
normal at M0; therefore,
it is also the locus of the centres of the circles passing by O
and tangent to the curve (G0);
the isotel is thus none other than the curve the orthotomic
of which is the initial curve, in other words, its "anti-orthotomic".
Since the orthotomic is the image of the pedal by a homothety with centre O and ratio 2, the isotel is none other than the image of the negative pedal by a homothety with centre O and ratio 1/2; the notion therefore became obsolete. |
 |
Conclusion: up to homothety, isotel = negative pedal = orthocaustic.
Examples:
- the parabola is the isotel of its directrix with respect to its focus.
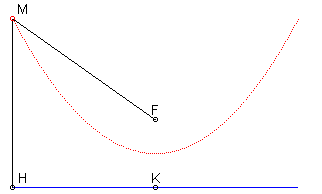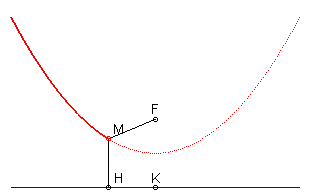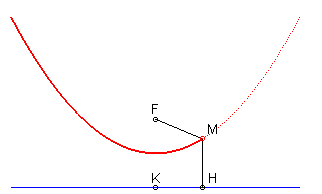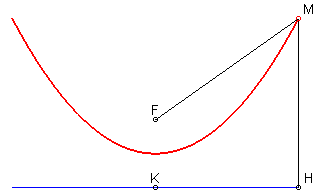
- a centred conic is the isotel of the directrix circle at one focus with respect to the other focus.
- the isotel curve of the ellipse with
respect to its centre is the Talbot curve.
For other examples, see negative
pedal.
| The isotel with respect to O of a curve of constant width has a remarkable property discovered by Euler (Nova Acta Eruditorum, 1746) : any ray coming from O reflected twice by the isotel goes back through O. Euler designates by catoptrix a curve having this property. The reader will note on the figure that the ray resulting from O is reflected well in M following MN, then in N according to NO. In addition, as OM+MN+NO=M0M+MN+NN0=M0N0, the distance traveled by the radius OMNO is constant, equal to the width of the starting curve. | 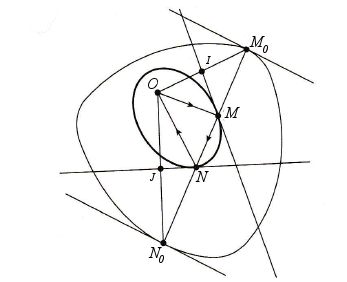 |
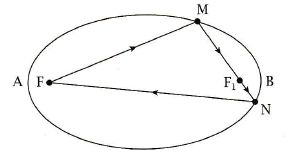
| The case of the isotel of a circle, which is an ellipse of focal point O is an obvious case of this property since any ray coming from a focal point is reflected in a ray passing through the other focal point. |
 |
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2020