COURBE DE PRÉCESSION CONSTANTE
Curve
of constant precession, Kurve konstanter Präzession

| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
COURBE DE PRÉCESSION CONSTANTE
Curve
of constant precession, Kurve konstanter Präzession

| Courbe étudiée par Paul D. Scofield en 1995. |
| Paramétrisation cartésienne : Courbe tracée sur l'hyperboloïde
: |
Les courbes de précession constante sont les courbes telles que le vecteur de rotation instantanée du repère de Frenet possède un mouvement de rotation uniforme autour d'un axe fixe lorsque ce repère parcourt la courbe à vitesse constante. Ce vecteur a donc un mouvement similaire à celui de l'axe d'une toupie, d'où l'expression "précession constante".
Rappelons que si le repère de Frenet est noté ,
le vecteur de rotation instantanée
est défini par les relations :
et donné par la formule :
.
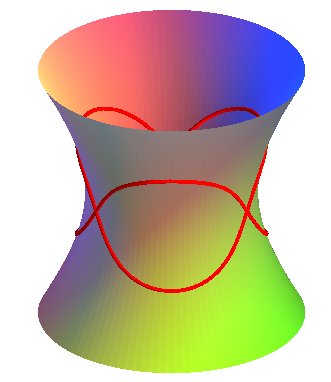
| La projection sur le plan xOy de la courbe donnée
ci-dessus est une épitrochoïde
de paramètre Ci-contre, le cas k =3/5 donnant q = 3.
|
 |
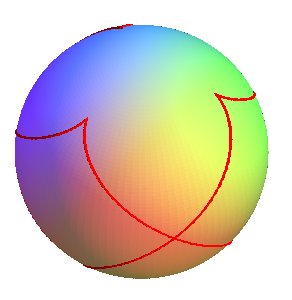
| L'extrémité du vecteur tangent décrit
l'indicatrice sphérique
de courbure de la courbe ; les formules montrent que cette indicatrice est une hélice sphérique. Ci-contre, l' indicatrice de courbure de la courbe ci-dessus. |
 |
Comparer avec les courbes
de Caparéda.
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2012